Category: Synthesis AI

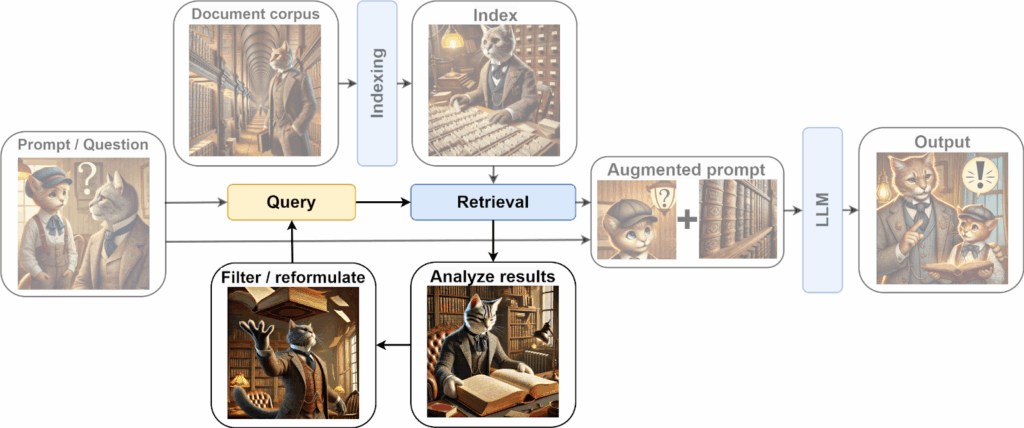
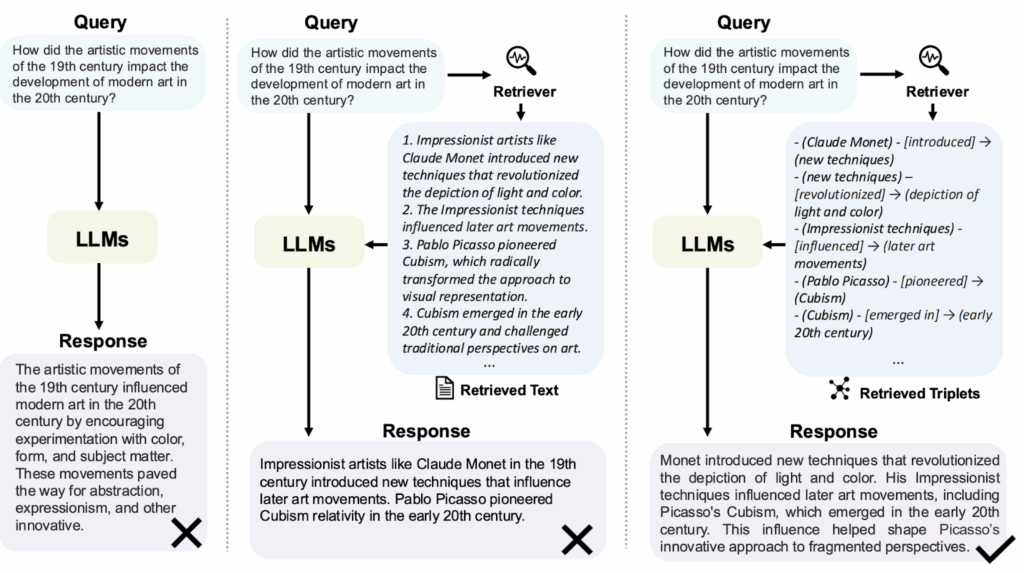
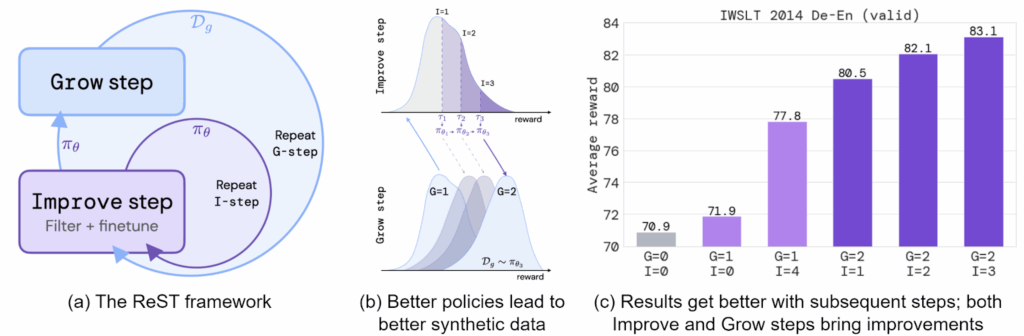
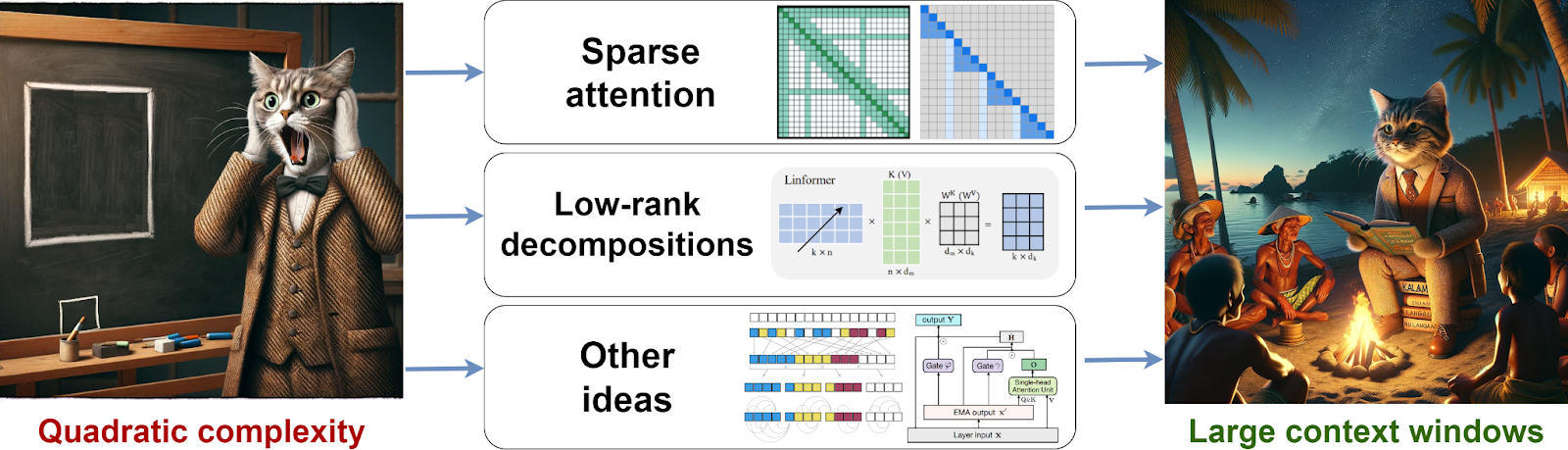
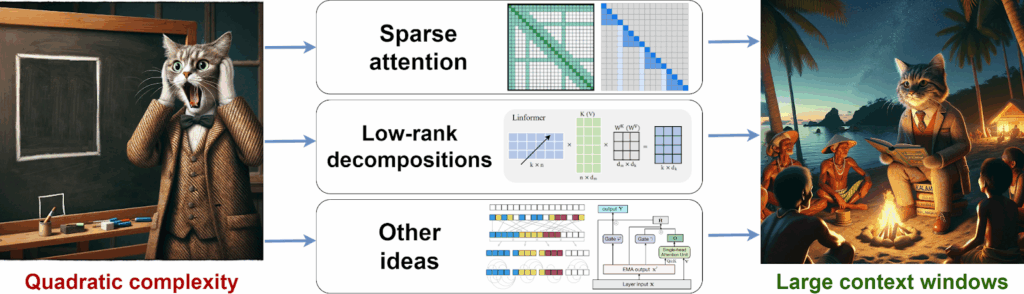
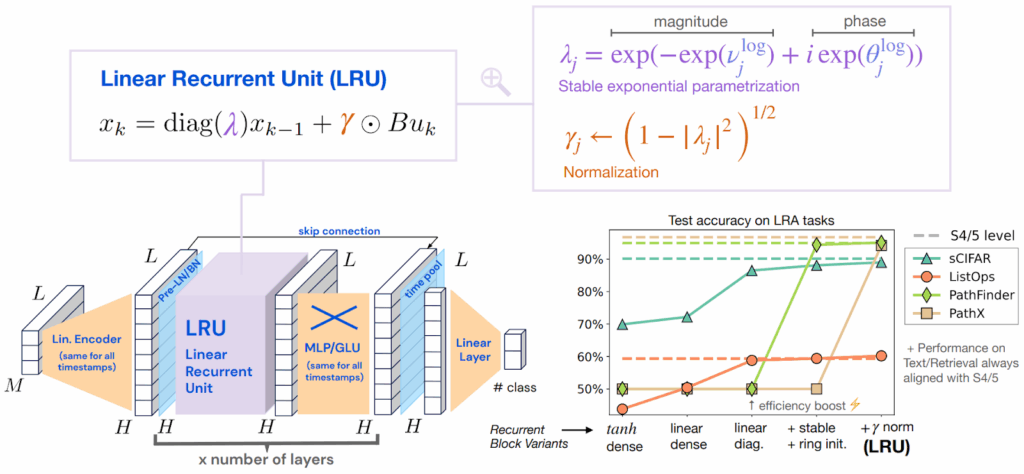
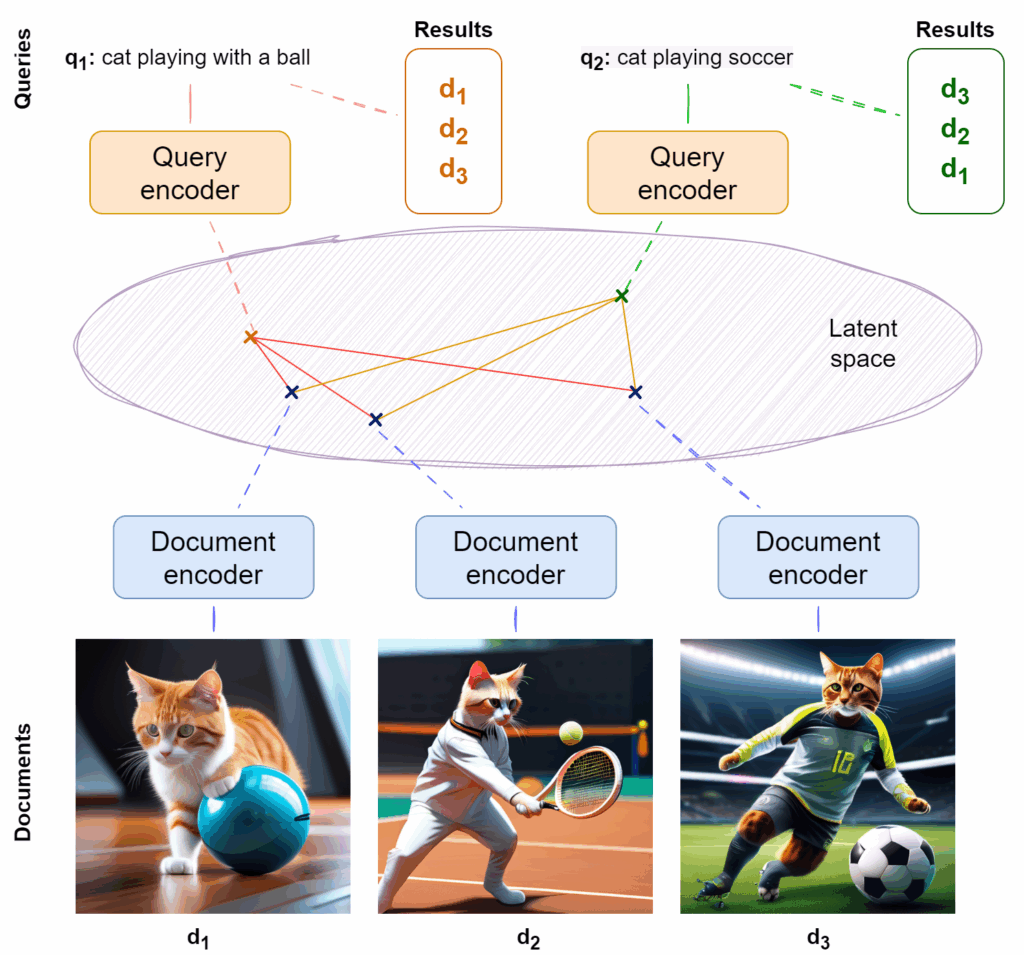
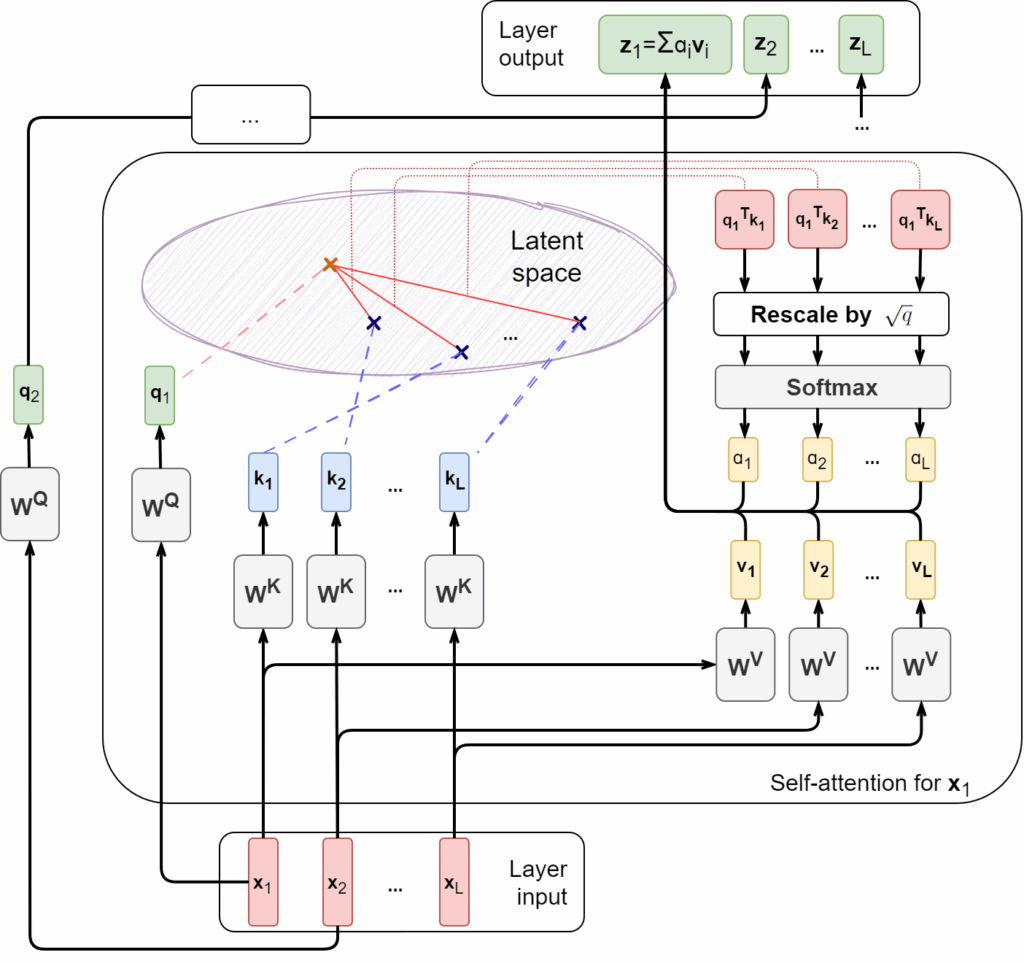
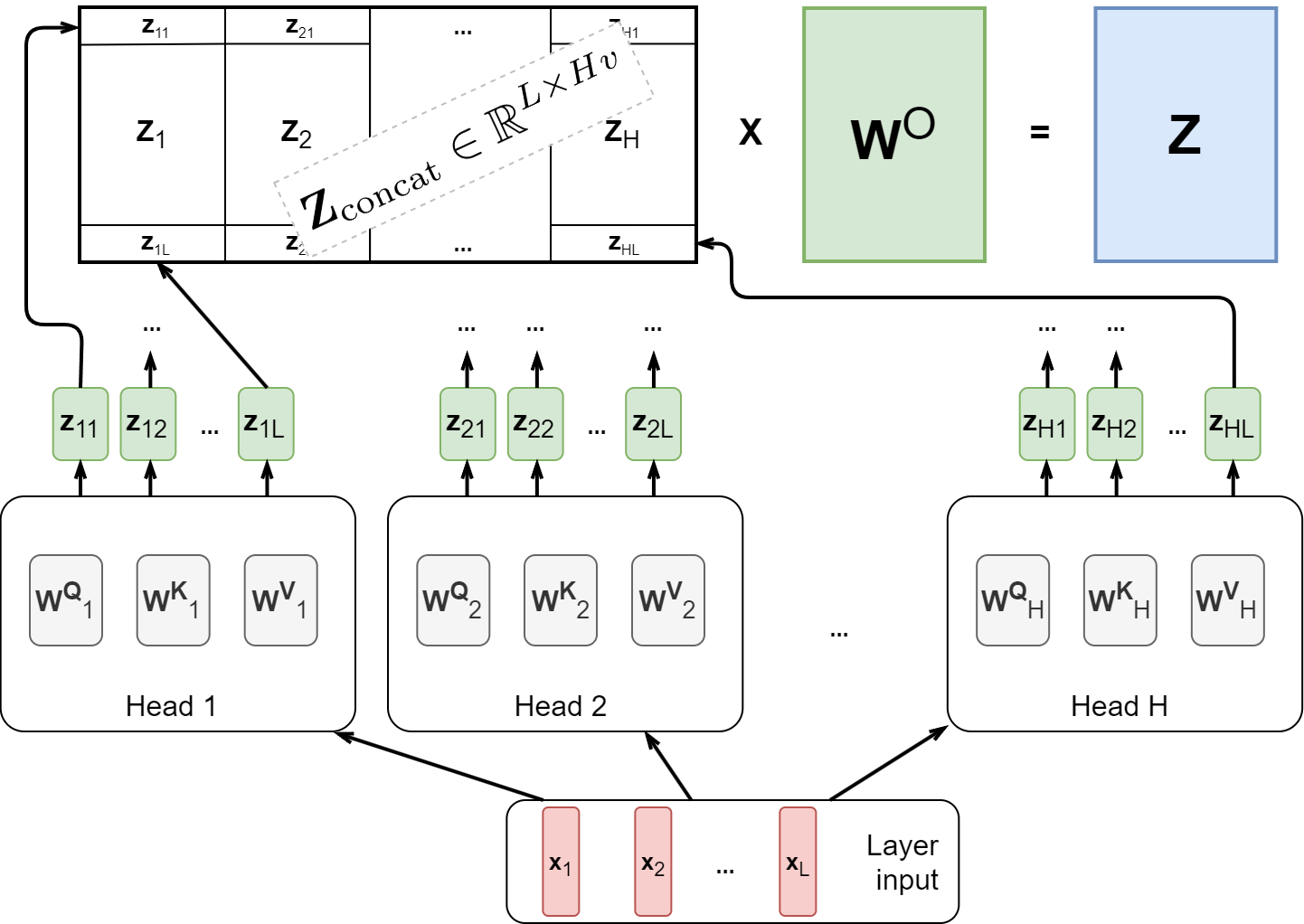
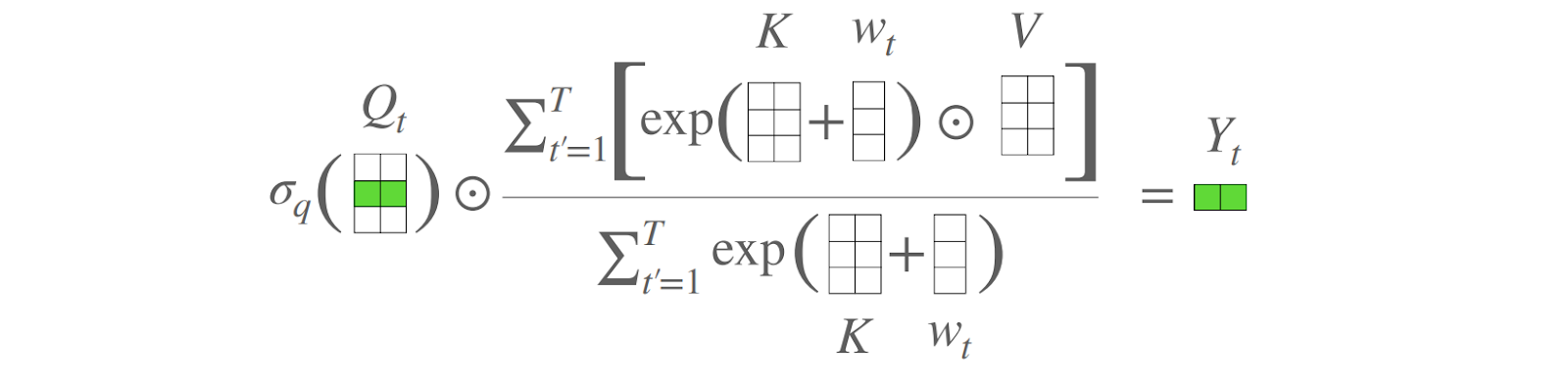We have already discussed how to extend the context size for modern Transformer architectures, but today we explore a different direction of this research. In the quest to handle longer sequences and larger datasets, Transformers are turning back to the classics: the memory mechanisms of RNNs, associative memory, and even continuous dynamical systems. From linear attention to Mamba, modern models are blending old and new ideas to bring forth a new paradigm of sequence modeling, and this paradigm is exactly what we discuss today.

Introduction: Explaining the Ideas

We have already discussed at length how Transformers have become the cornerstone of modern AI, powering everything from language models to image processing (see a previous post), and how the complexity of self-attention, which is by default quadratic in the input sequence length, leads to significant limitations when handling long contexts (see another post). Today, I’d like to continue this discussion and consider the direction of linear attention that has led to many exciting advances over the last year.

In the several years of writing this blog, I have learned that it is a futile attempt to try to stay on top of the latest news in artificial intelligence: every year, the rate of progress keeps growing, and you need to run faster and faster just to stay in one place. What I think still matters is explaining ideas, both new ideas that our field produces and old ideas that sometimes get incorporated into deep learning architectures in unexpected ways.

This is why I am especially excited about today’s post. Although much of it is rather technical, it allows me to talk about several important ideas that you might not have expected to encounter in deep learning:

• the idea of linear self-attention is based on reframing the self-attention formula with the kernel trick, a classical machine learning technique for efficiently learning nonlinear models with linear ones (e.g., SVMs);
• then, linear attention becomes intricately linked with associative memory, a classical idea suggested in the 1950s and applied to neural networks at least back in the 1980s in the works of the recent Nobel laureate John Hopfield, and fast weight programmers, an approach developed in the early 1990s;
• finally, Mamba is the culmination of a line of approaches based on state space models (SSM), which are actually continuous time dynamical systems discretized to neural architectures.

Taken together, these techniques represent a line of research… well, my first instinct here was to say “an emerging line of research” because most of these results are under two years old, and Mamba was introduced in December 2023. But in fact, this is an already pretty well established field, and who knows, maybe this is the next big thing in sequence modeling that can overcome some limitations of basic Transformers. Let us see what this field is about.

Linear Attention: The Kernel Trick in Reverse

As we have discussed many times (e.g., here and here), traditional Transformers use softmax-based attention, which computes attention weights over the entire input sequence:

   

This formula means that serves as the measure of similarity between a query and a key (see my previous post on Transformers if you need a reminder about where queries and keys come from here), and one important bottleneck of the Transformer architecture is that you have to compute the entire matrix of attention weights. This quadratic complexity limits the input size, and we have discussed several different approaches to alleviating this problem in a previous post.

Linear attention addresses this problem with a clever use of the kernel trick, a classical idea that dates back to the 1960s (Aizerman et al., 1964). You may know it from support vector machines (SVM) and kernel methods in general (Schölkopf, Smola, 2001; Shawe-Taylor, Cristianini, 2004; Hofmann et al., 2008), but you also may not, so let me begin with a brief explanation.

Suppose that you have a linear classifier, i.e., some great way to find a hyperplane that separates two (or more) sets of points, e.g., a support vector machine that finds the widest possible strip of empty space between two classes:

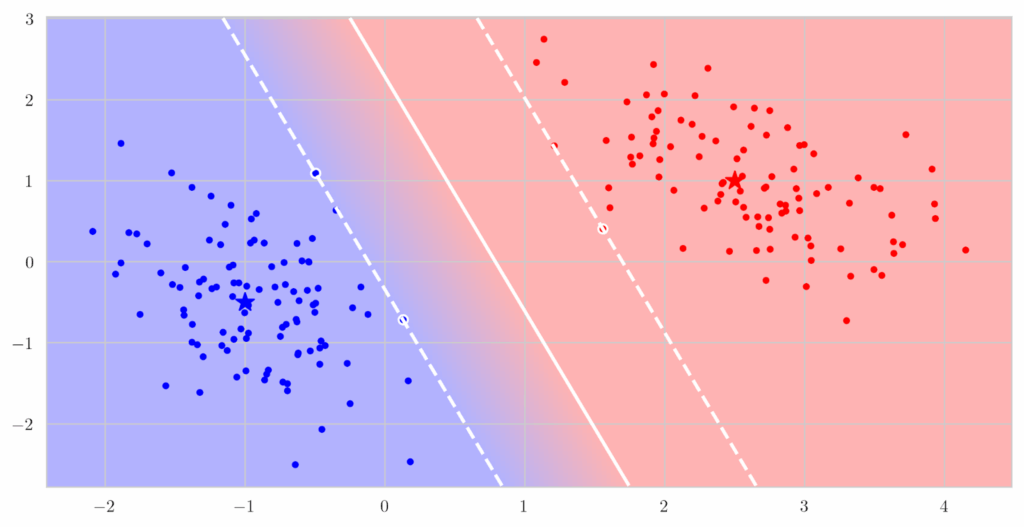
But in reality, it may happen that the classes are not linearly separable; for instance, what if the red points surround the blue points in a circle? In this case, there is no good linear decision surface, no hyperplane that works, and linear SVMs will fail too:

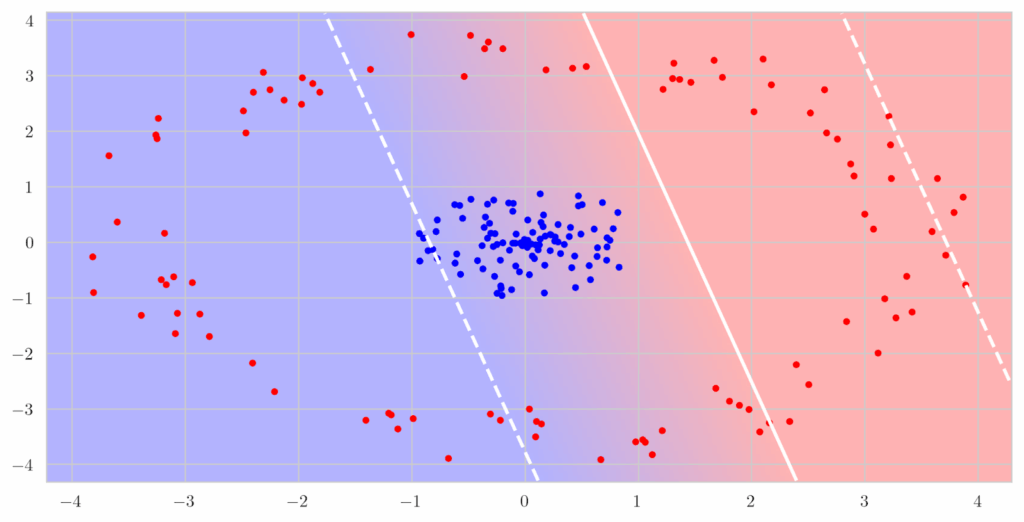
But it is also quite obvious what a good decision boundary would look like: it would be a quadratic surface. How can we fit a quadratic surface if we only have a linear classifier? Actually, conceptually it is quite easy: we extract quadratic features from the input vector and find the linear coefficients. In this case, if we need to separate two-dimensional points , a quadratic surface in the general case looks like

   

so we need to go from a two-dimensional vector to a five-dimensional one by extracting quadratic features:

   

In the five-dimensional space, the same formula is now a linear surface, and we can use SVMs to find the best separating hyperplane in that will translate into the best separating quadratic surface in :

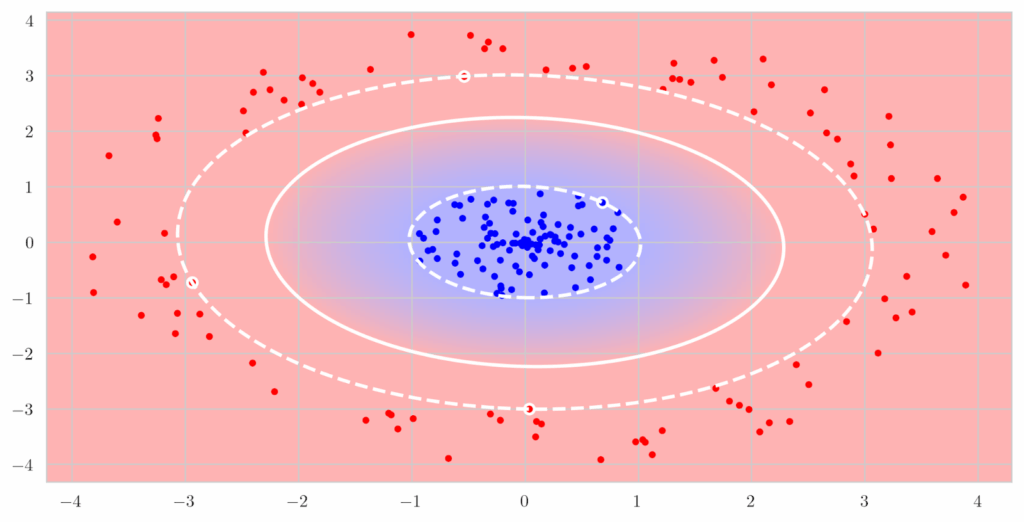
You can use any linear classifier here, and the only drawback is that we have had to move to a higher feature dimension. Unfortunately, this is a pretty severe problem: it may be okay to go from to but even if we only consider quadratic features as above it means that will turn into , which is a much higher computational cost, and a higher degree polynomial will make things much worse.

This is where the kernel trick comes to the rescue: in SVMs and many other classifiers, you can rewrite the loss function in such a way that the only thing you have to be able to compute is the scalar product of two input vectors  and (I will not go into the details of SVMs here, see, e.g., Cristianini, Shawe-Taylor, 2000). If this property holds, instead of directly going to the larger feature space we can look at what computing the scalar product means in that space and probably find a (nonlinear) function that will do the same thing in the smaller space. For quadratic features, if we change the feature extraction function to 

   

(this is a linear transformation that does not meaningfully change our classification task), we can rewrite the scalar product as 

   

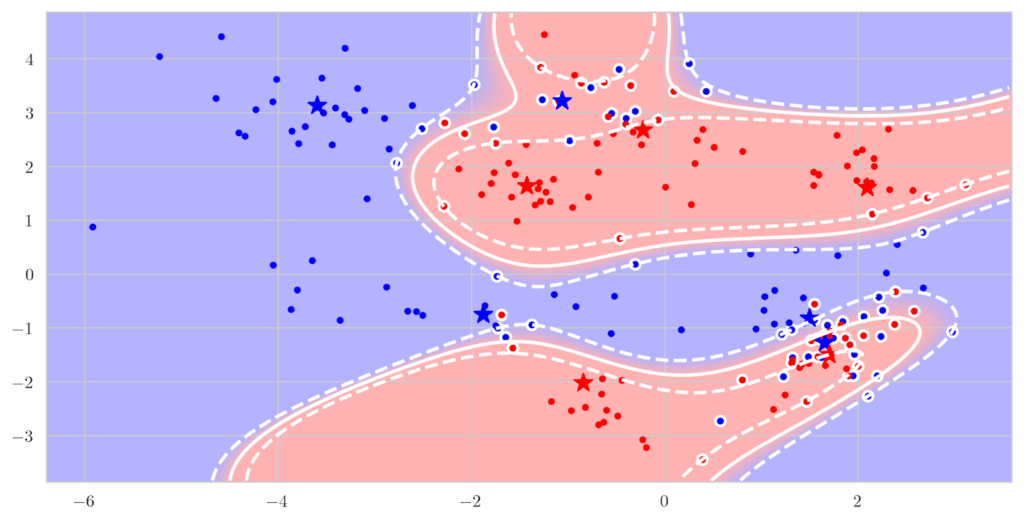
The result is called a kernel function , and we can now replace scalar products in the higher-dimensional space with nonlinear functions in the original space. And if your classifier depends only on the scalar products, the dimension of the feature space is not involved at all any longer; you can even go to infinite-dimensional functional spaces, or extract local features and have SVMs produce excellent decision surfaces that follow the data locally:

Well, linear attention is the same trick but in reverse: instead of using a nonlinear function to represent a high-dimensional dot product, let us use a feature extractor to approximate the nonlinear softmax kernel! We transform each key and query using a feature map , so that similarity between them can be computed as a dot product in feature space, ; let us say that maps the query and key space to . So instead of computing each attention weight as the softmax

   

(I will omit the constant  for simplicity; we can assume that it is incorporated into the query and key vectors), we use a feature map, also normalizing the result to a convex combination:

   

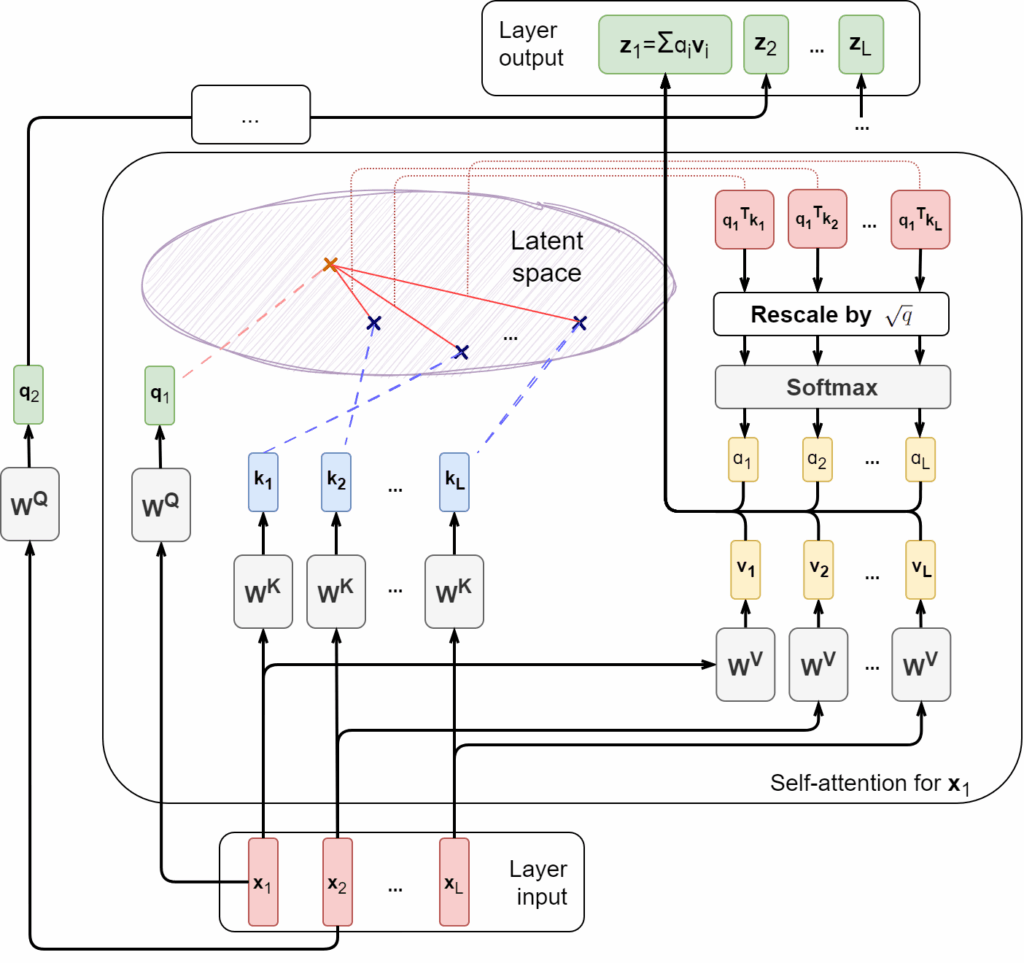
This is much more convenient computationally because now we can rearrange the terms in the overall formula for , and the quadratic complexity will disappear! Like this:

   

Now instead of computing the matrix of attention weights we can first multiply by (getting the brackets in the numerator above), which is a multiplication of and matrices, and then reuse it for every query, multiplying the matrix by the result:

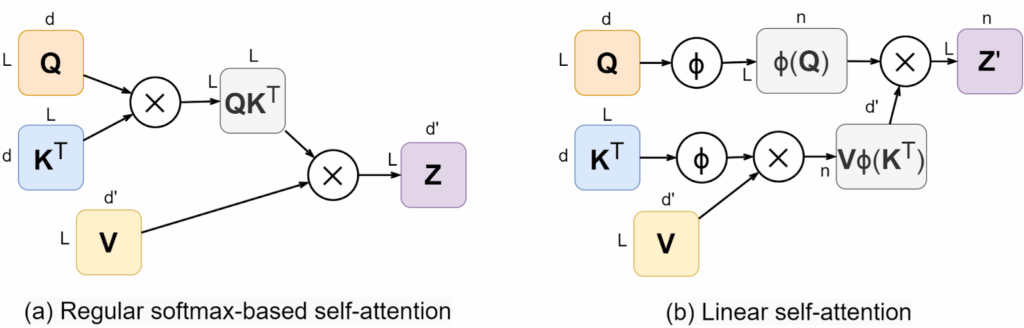
Note that the result has dimension rather than , and also note that I put as the output in the (b) part of the figure (on the top right) because it is only the numerator of the fraction above, but the denominator is also obviously not quadratic: we can first add up and then multiply by each query. Let us also simplify the formula above by denoting

   

so we get a simple formula for linear attention as

   

This is exactly the idea of linear attention as proposed by Katharopoulos et al. (2020). But there is one more important step.

Causal Linear Attention: Transformers are RNNs?

We know that Transformers are often applied autoregressively. Any language model, e.g., from the GPT family (recall our post on Transformers), is an autoregressive model that applies self-attention to the same sequence gradually, step by step, and causally: an output at position depends only on inputs in positions .

To train an autoregressive Transformer, you don’t have to rerun the whole model for every token, like you do for generation. Instead, autoregressive Transformers use causal self-attention, a special modification where the entire sequence is input at once, but the attention weights to future tokens are automatically set to zero. This means that we get the same self-attention formula but with sums only going up to the current -th token:

   

Passing to a scalar product with feature extractor as above, we get

   

It is becoming more and more clear where this is going: since and are just cumulative sums, we don’t have to recompute them from scratch on inference; instead, we can update them from previous values as

   

Katharopoulos et al. (2020) also show that the gradients can be computed incrementally from timestep to timestep; this is a straightforward calculation so I will not repeat it here. As a result, they come to the conclusion that their linear Transformer is… essentially a recurrent neural network (RNN)! This “RNN” has a hidden state that consists of two different components, a matrix state and a normalizer state ; we have derived the formulas for how to update this recurrence above, and we also know the formula for the output of this recurrent layer:

   

In practice, one often removes the normalizing denominator since it can lead to numerical instabilities (Schlag et al., 2021; Mao, 2022), and the feature extractor is commonly taken to be , so the formulas simplify to

   

But isn’t that a little too simple? Linear attention uses the kernel trick to approximate the softmax mechanism efficiently, enabling Transformers to handle longer sequences. However, this shift from quadratic to linear complexity raises questions about the fundamental role and meaning of attention: how should models store and retrieve relevant information efficiently? In the next section, we discuss associative memory, a classical concept in neural networks, which in this case turns out to be an important point of view on this question. In particular, it shares a similar goal of learning to store patterns and retrieving them based on input queries. By revisiting associative memory, we can better understand the underlying mechanisms of linear attention and their limitations.

Fast Weight Programmers and Associative Memory

We discuss several approaches in this section but mostly follow Schlag et al. (2021) who provide us with some key intuition about linear Transformers. They note that linear Transformers are almost entirely equivalent to an architecture called Fast Weight Programmers (FWPs), developed by Jurgen Schmidhuber (yes, this was his idea too!) in the early 1990s (Schmidhuber, 1992; 1993).

FWPs come from the basic intuition that the weights in standard neural networks remain fixed after training; activations change depending on the input, but the weights themselves are frozen. This is a bad thing for what is known as the binding problem (Greff et al., 2020): a neural network has no easy way to bind variables, define symbols, and thus construct compositional internal representations and perform symbolic reasoning that plays a key role in human cognition (Whitehead, 1927; Spelke, Kinzler, 2007; Johnson-Laird, 2010).

One possible solution for the binding problem would be to have two kinds of weights in a neural network: slow weights that are fixed after training as usual and fast weights that are context-dependent and can change on inference. As Greff et al. (2020) put it, “the slow net learns to program its fast net”. In an FWP (Schmidhuber, 1991; 1992), the slow network learns to adjust fast weights as follows: for a sequence of inputs , ,

   

where and are slow weights and are fast weights. In essence, fast weights play the role of an RNN’s hidden state and the formulas above define the recurrence (Schmidhuber himself rephrased this idea in recurrent terms a year later, in 1993).But note the uncanny resemblance of this update rule and Transformer’s self-attention: Schmidhuber’s FWPs also make use of the outer produce to update the hidden state! FWPs create a short-term associative memory where keys are associated with values in a matrix form, the write operation is implemented by adding the outer product, and the readout is represented by matrix multiplication.

You can see how this resemblance becomes a formal equivalence when we move to linear attention: if we set the activation function σ above to identity, we get exactly the update rule and readout of simplified linear attention:

   

Normalization (the vector  above) was absent from the FWPs of the 1990s but it also a straightforward idea in this formulation: whenever you have a “memory” that accumulated a big sum of values along the input sequence, it is natural to try and renormalize the sum to keep it at the same scale.

To make further improvements, Schlag et al. (2021) also go back to the original motivation for the whole thing: fit information into the hidden state matrix . The relation to fast weight programmers also brings back the original goal of this transformation: we store vectors in the matrix , and then retrieve this information via matrix multiplication. Let us discuss this in more detail.

The idea of storing information in this way is known as associative memory, a classical concept in artificial intelligence (see, e.g., Haykin, 2011) which is a natural generalization of, well, just storing things in memory:

• in regular memory, you have d slots where you can store something (say, a vector), and retrieval from the memory can be thought of as multiplying the memory matrix by a vector; storing something new in regular memory can be thought of as adding a rank one matrix with the new vector in its proper slot;
• in associative memory, you have a matrix that stores vector associations as projections to some orthogonal basis; to store a new association in the matrix , you need to choose a key vector  that’s orthogonal to previous key vectors and update ; to retrieve the association, you do a projection by multiplying .

Associative memory is another one of those ideas that were motivated by neurobiology and date back to early studies of the brain. In 1949, Donald Hebb introduced his famous learning principle, often summarized as “neurons that fire together, wire together” (Hebb, 1949); in other words, associations between neurons, reflected in synapse weights, grow stronger if neurons get activated at the same time. Unlike gradient descent, Hebbian learning is actually possible with biological neurons, and Hebb’s work in many ways remains relevant in neurobiology today (his theory also made provisions for, e.g., spike-timing-dependent plasticity that was not known in the 1940s).

It soon became clear that associative memory could be used as a kind of machine learning model. Early attempts at such models started in the 1950s (Taylor, 1956), but two ideas based on associative memory found wide success later:

• self-organizing maps (SOM), or Kohonen networks, developed by Teuvo Kohonen in the 1970s (Kohonen, 1974), were at some point among the most popular unsupervised learning methods, performing representation learning by adjusting the weights towards neurons that are already best matches for the input, a process known as competitive learning (Grossberg, 1987; Kohonen, 1988);
• Hopfield networks, developed by John Hopfield in the 1980s (Hopfield, 1982; 1984), store patterns in minima of energy landscapes of neural networks and retrieve them by evolving towards these local minima, which means that retrieval is done by association from incomplete data; there has been a lot of research on Hopfield networks (Krotov, Hopfield, 2016; 2020; Demircigil et al., 2017; Ramsauer et al., 2020), and recently John Hopfield shared the 2024 Nobel Prize in Physics with Geoffrey Hinton for his work in neural networks, but this is a story for another time.

Let us walk through an example of how associative memory works. We will work in 2D so that we can plot everything, so we begin with a zero matrix . Suppose that we want to store two vectors in that matrix,

   

If we were just storing them in the matrix column by column, it would be equivalent to using keys aligned with coordinate axes:

   

Reading from this memory is simply reading the columns, or, equivalently, multiplying by (1 0) and (0 1) key vectors. But we can take any other set of two orthogonal key vectors, say (let’s keep them at unit length to avoid renormalization):

   

In this case, we get

   

Reading from this matrix still works fine:

   

But if you try to add a third vector to the same associative memory with a third key, which is now inevitably non-orthogonal with the first two, say,

   

retrieval results will become corrupted, both for the original vectors and for the new vector :

   

Geometrically this effect can be illustrated as below; we can find two orthogonal vectors for the first two keys (on the left in the figure) but the third one breaks perfect retrieval (retrieved vectors are shown with dashed lines on the right):

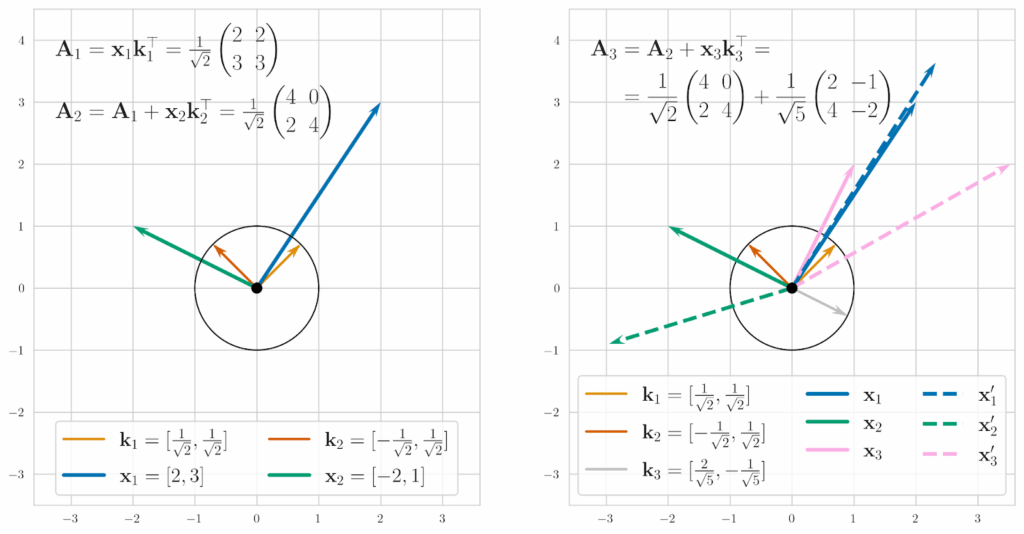
So far, it doesn’t sound like much of an improvement: we could just store vectors row by row and have the exact same number of them fit. The point of associative memory lies in its robustness to the orthogonality requirement: if the keys are nearly orthogonal you will retrieve vectors that are still quite similar to the originals, even if the keys are not orthogonal exactly. And this means that we can fit more keys than the matrix dimension, with imperfect but still reasonable recall!

This is hard to illustrate with a two-dimensional picture but in high dimensions you can use sparse keys that are all nearly orthogonal even though they intersect a little. For example, if , and you use binary keys that all look like a vector with  ones and 90 zeros (divided by , of course), two keys that have zero ones in common are perfectly orthogonal with zero dot product, but the keys that have only one in common have the dot product of 1/10, which may be sufficient for retrieval in practice.

Finding out how many such keys can exist for given d, k, and m is a well known problem from a completely separate field of study, called the theory of block designs, a part of the theory of error-correcting codes. This is essentially a coding question: how many codewords with at most a given intersection can you fit for a given dimension, given codeword weight (number of ones), and given intersection constraint? I will not go into error-correcting codes and refer to, e.g., (Assmus, Key, 1992; Huffman, Press, 2003), but the main relevant results here are the Hamming bound that is proven by counting and the more complicated Johnson bound. The Hamming bound says that without restrictions on the weight, for given d and m you can fit about

   

binary keys. We are interested in large values of m, where you can get a good approximation for the denominator via the entropy of the relative distance:

   

This means that even if you require small intersections, you can fit an exponential number of codewords, just with a smaller exponent. The Johnson bound deals with vectors of fixed weight, and we will not go there now, but the point stands: you can fit a lot of codewords with small intersections, asymptotically much more than d, and this gives us a way to store a lot of vectors in associative memory as long as we are okay with imperfect retrieval.

Now we have a much better intuition for what is going on in linear attention Transformers. But where will the improvements come from?

Improving Linear Transformers

While linear Transformers are more efficient than classical self-attention and reduce its complexity from quadratic to linear, this efficiency comes at a cost. Linear attention approximations can struggle with tasks that require precise content-based reasoning or long-term memory, and further research is clearly needed.

How can we improve upon the architecture above? We have already seen that the kernel can be different. But once you start thinking about updates to as storing key-value pairs in memory, the update itself also becomes a promising point of possible new approaches: maybe summation is not the best way to store things in memory?

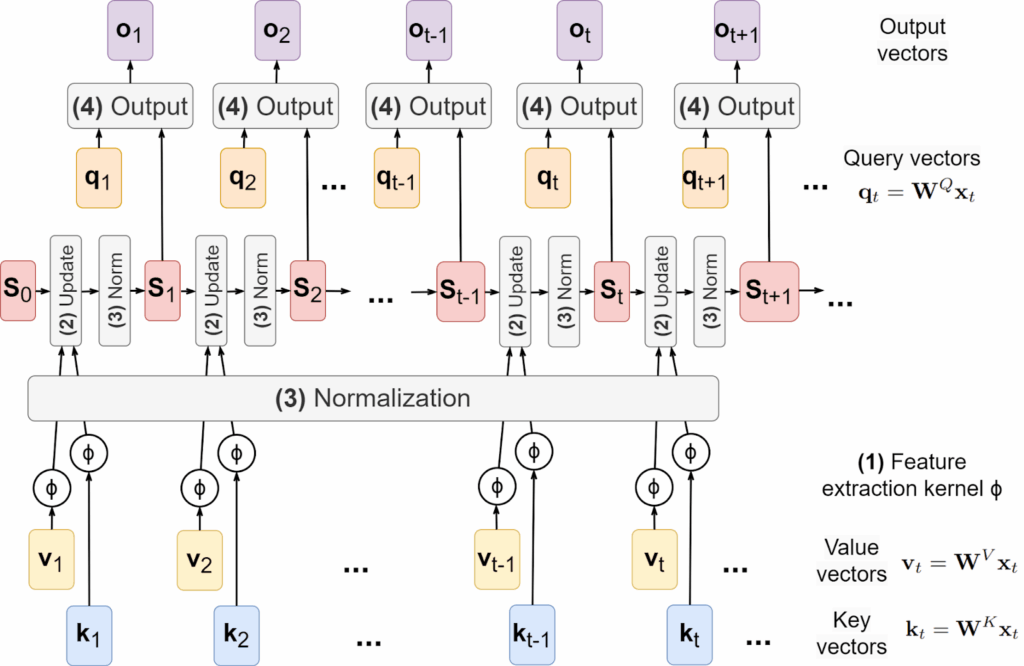
So at this point, we see that the linear self-attention structure breaks down into four decisions, each of which can suggest directions for improvement:

• the nonlinear transformation of the key and value vectors before storing them in ;
• the memory update rule for itself; let us call it : ;
• the normalization mechanism, which so far has been either absent or via direct accumulation in the vector ; in theory, we could normalize the key, value, and query vectors separately, or just normalize the hidden state;
• the mechanism for producing the output vector from the query and the hidden state matrix .

I have illustrated the general scheme below, showing where these different items go in the architecture. Let us now consider these directions one by one.

First, for the nonlinear transformation Katharopoulos et al. (2020) suggested to use either the identity function or the exponential linear unit ELU, a variation of ReLU with nonzero derivative everywhere (plus one to make nonnegative):

   

Here is basically an activation function, operating independently on every component of and . However, in the previous section we motivated the function as an approximation to the numerator of softmax, i.e., we would ideally want

   

which is definitely not the case for ELU+1.

The Performer architecture (Choromanski et al., 2021) introduced a version of which is a much better approximation for softmax. They provide a detailed proof that we will not reproduce here, but in essence their approach, called FAVOR+ for Fast Attention Via positive Orthogonal Random features, uses random linear transformations in such a way that the expected result is indeed the softmax kernel shown above: they define

   

where is an random matrix whose every row is drawn from the standard Gaussian in dimension , and prove that the expectation of coincides with the softmax kernel , and that

   

Schlag et al. (2021) introduce the so-called deterministic parameter-free projection (DPFP), an approach where components of are constructed to be orthogonal by design: if then for all other than . This can be achieved with ReLU activations if you just design them so that their nonnegative areas do not overlap. For example, can map to as follows:

   

where is the ReLU activation function. Note how regardless of the input vector all components of except one are zero because either or is always zero. The authors generalize this approach to higher dimensions as well; note that ReLUs are also very computationally efficient, much more so than computing exponents.

Second, let’s turn to the memory update rule. As the number of vectors stored in associative memory increases over the matrix dimension d, the memory mechanism should ideally figure out which vectors to “overwrite”. This is especially important because in practice, you may get a new key-value pair that is similar to an already existing key that points to an already similar value, in which case you don’t really want to overwrite anything at all but rather update the value a little so that both keys will retrieve a good enough approximation of it. 

Schlag et al. (2021) propose the following approach here: for a new key-value pair , retrieve that is already stored in memory by the key (you can always do retrieval in associative memory, if we are not yet at memory capacity it will just return zero) and store a convex combination of and . The coefficient of this combination, the “overwrite force” for this vector, can also be derived from the inputs. Formally, we define

   

and then in the matrix state computation we erase from memory and write in , getting

   

Third, for normalization you can use attention normalization as suggested by Katharopoulos et al. (2020) or, for instance, sum normalization where query and key vectors are divided by the sums of their own components. Normalization can be done only at the level of queries, keys, and values, or also at the output o_t, and so on, and so forth.

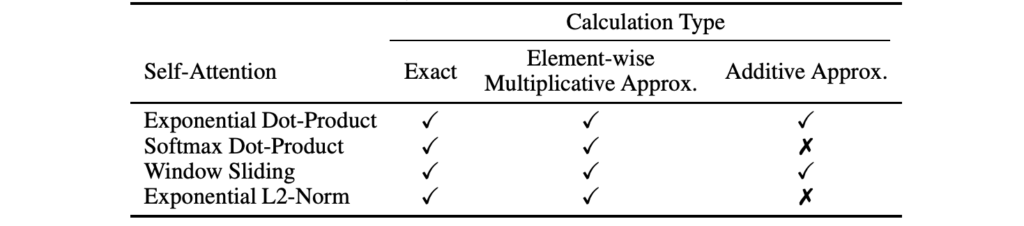
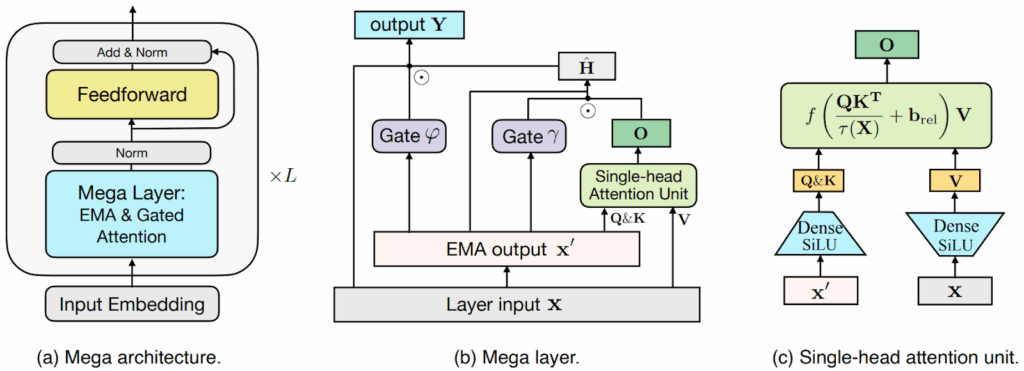
The possibilities are endless, and indeed, one can think of a lot of different modifications for the above formulas. Some of them explore different feature functions, others change how combinations and moving averages are computed, yet others add various gates to the architecture up to the complexity of an entire LSTM (Peng et al., 2021; Beck et al., 2024). The summary table below is taken from a recent work by Yang et al. (2024), which in turn proposes yet another approach in this vein:

Naturally, I don’t want to go over the entire table here; we are already acquainted with several rows in this table enough that you can mostly understand the motivation behind the others. But there is one more important direction that leads to interesting new ideas and that has been growing in popularity lately, so I want to explore it in more detail.

Mamba: Transformers are State Space Models

While linear attention provides a scalable alternative to Transformer’s self-attention, it still struggles with tasks requiring explicit reasoning over long-term dependencies or fine-grained temporal dynamics. In this section, we discuss state space models that provide an alternative perspective: instead of focusing on approximating attention, they model sequences as evolving states governed by differential equations. This still allows the system to handle long-range dependencies while at the same time learning structured dynamics inspired by control theory.

To explain what is going on in Mamba, we need to take a step back yet again, this time to state space models. A state space model (SSM) is another way to process sequential input, very similar to RNNs in that an SSM also has a hidden state that is supposed to capture all relevant information about the current state of the system. But the state space model looks at system evolution from a continuous standpoint, considering the dynamical system

   

Here is an illustration:

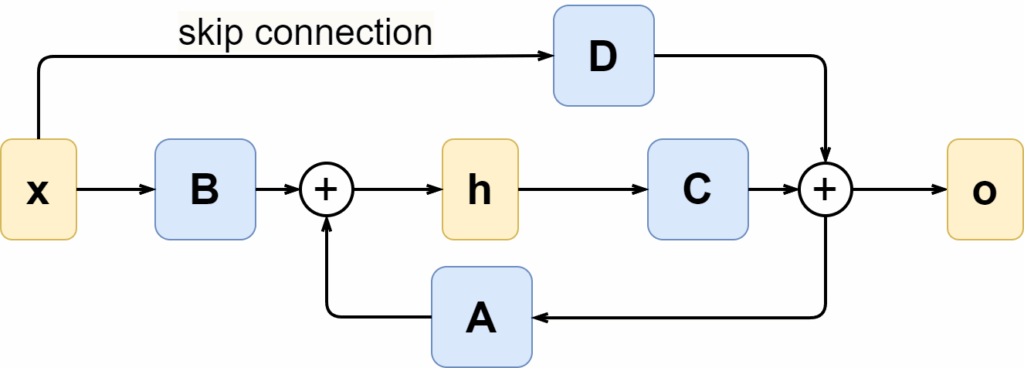
Note that the direct dependence of the output o(t) on the input x(t) can be thought of as a skip connection going around the dynamical system, so below we will assume that D=0.

This approach has its roots in control theory; the famous Kalman filter (Kalman, 1960) is a special case of SSMs, and classical control theory has a lot of results on such linear dynamical systems (Jazwinski, 1970; Kailath, 1980), spilling over into econometrics and generally time series analysis (Hamilton, 1994). 

The equations above look just like a classical RNN; the main difference is that they are continuous, so we can hardly expect to be able to work with them unless we can discretize continuous signals and vice versa, turn discrete inputs (such as text) into continuous signals. In this approach, it is usually enough to consider the zero-hold model, where a discrete input is turned into a set of step functions with step size Δ, and a continuous signal is sampled according to the input timesteps. Discretization of dynamical systems proceeds via matrix exponentials that result from solving the differential equations above on an interval , where the input can be assumed constant, so the solution is

   

As a result, we can define discretized versions of the matrices and (see, e.g., Grootendorst, 2024 for a more detailed explanation) as

   

and treat this discretized version of an SSM as a linear RNN with update rule (omitting as discussed above)

   

Note that this is not the only way to do discretization, for example, Gu et al., 2022 use a bilinear method where

   

Moreover, doing everything via discretizations of continuous functions has other advantages; for example, we can seamlessly handle missing data by simply continuing the discretization over a longer time period (where we do not have new data).

Finally, we can also note that in this formulation, every output can be easily represented as a series depending on the inputs :

   

which can be thought of as a convolution operator: to get , we convolve the input series with the kernel

   

 is called the SSM convolution kernel, and if it is known, the SSM can be very efficiently computed in parallel during training, when we have the entire input sequence available, just like any autoregressive model. Computing , however, is a nontrivial task that also requires new tricks.

But whatever the discretization formulas, the resulting RNN will not really work as intended. This is a classical approach that has been well-known for decades, and, of course, people have tried to apply it to machine learning. But they had always found this approach to lack long-term memory because of vanishing and/or exploding gradients due to all of this matrix multiplication, which is precisely the point of having a recurrent network in the first place.

To add long-term memory, we need one more technique developed by Gu et al. (2020): we need to replace the matrix  with the so-called “HiPPO matrix”, where HiPPO stands for high-order polynomial projection operators. The HiPPO approach begins with a different question: how do we compress the entire history of an input function , namely , into a functional representation? The core idea is to approximate the function of by projecting it onto a space spanned by orthogonal polynomials. With this approach, HiPPO can handle long-range dependencies without needing explicit priors on the timescale, which is crucial for data with unknown or variable temporal scales.

Without going into too much mathematical details (for those, see the original paper), HiPPO operates as follows: for a function  where we are interested in operating on its current history , 

• define approximation quality in the space of (square integrable) functions via a probability measure μ; this measure can be used to give recent information more weight than past history (or not);
• choose the approximation order  and choose a polynomial basis of degree ; HiPPO usually works with either Legendre polynomials and a uniform measure on the history (HiPPO-LegS) or Laguerre polynomials and an exponentially decaying measure (HiPPO-LagT);
• find the optimal approximation, i.e., find the coefficients of a polynomial  in the chosen basis that minimizes the approximation quality

     

• the whole point of HiPPO is that one can construct a differential equation to maintain these coefficients incrementally; for a vector of coefficients , you can write down matrices and such that

     

• and finally, this differential equation can also be discretized to find a recurrence on the polynomial coefficients for the optimal approximation of a discrete time series :

     

Here is an illustration from the original paper that shows this sequence of steps:

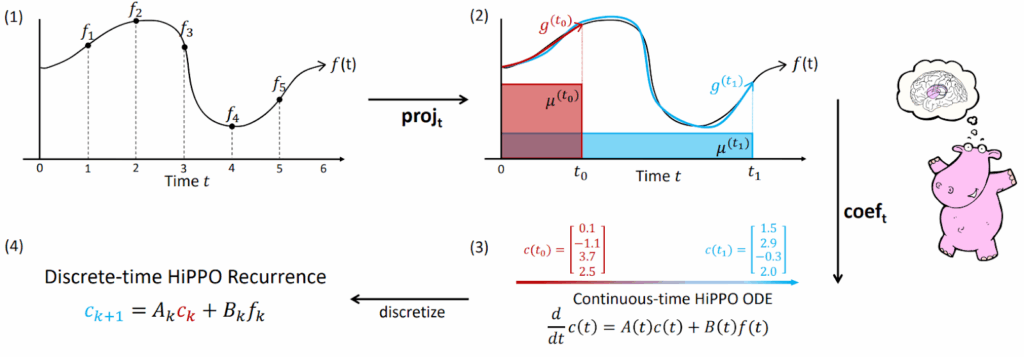
Gu et al. (2020) derive specific formulas for the HiPPO matrices. For their scaled Legendre measure (HiPPO-LegS) the matrix dynamics are

   

where  and  are constant:

   

and .

That was quite a lot of math that’s very different from what we are used to here—but bear with me, we are back to machine learning territory. At this point, we have a method that can take a time series as input and produce a good vector representation for its entire history; moreover, the method reduces to using a couple of matrices whose coefficients can be updated recursively with time too. This means that we can, for example, plug HiPPO into a regular RNN, adding another state c_t and replacing the hidden state h_t with a representation of its entire history; this has been done in the original paper on HiPPO as follows, for an arbitrary RNN update:

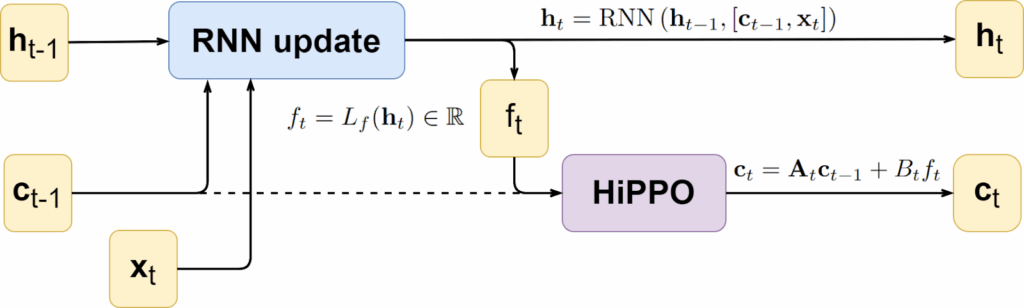
In SSMs, the HiPPO matrix is used to initialize the transition matrix A, significantly alleviating the problem of long-range dependencies. It may sound a little strange because as soon as we begin updating the weights, the matrix A loses its HiPPO properties: it no longer corresponds to the Legendre or Laguerre polynomials, or to any orthogonal basis in the functional space at all. However, experiments show that this initialization does help a lot with implementing long-term memory.

The second problem we need to solve is computational complexity: so far, SSMs require repeated multiplication by the discretized version of A, so the naive complexity is O(d²L), where d is the input vector dimension and L is the sequence length. The main contribution of the S4 model (structured state space sequence model) introduced by Gu et al. (2022) is a much faster way to compute all views of the SSM model, i.e., both recurrent matrices used at inference and convolutions used at training. The ideas of S4 would be way too mathy to put in this post; fortunately, I can refer to “The Annotated S4”, a detailed post by the S4 authors that shows all derivations and also provides the corresponding PyTorch code and illustrations. For now, let us just assume that all of the above can be done efficiently.

The next step was taken by Smith et al. (2022) who moved from single-input, single-output SSM layers to multi-input, multi-output layers, allowing x_t and o_t to become vectors; their model is known as S5 (simplified structured state space for sequence modeling).

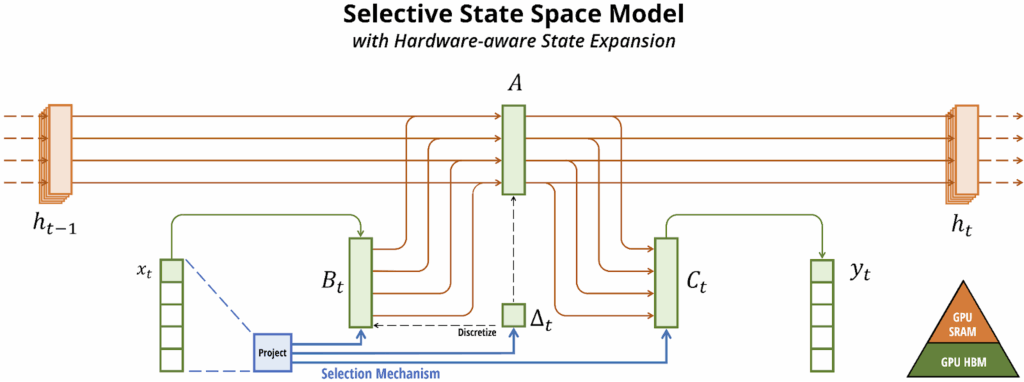
With this, we finally come to Mamba (Gu, Dao, 2024), also known as S6 (S4 + selective scan). The main step forward in Mamba is recognizing that so far, the model dynamics have had to be constant: matrices A, B, C, and step size Δ can be trainable from mini-batch to mini-batch but they cannot depend on the input x_t; otherwise, we wouldn’t be able to implement the convolutional kernel K which is key to efficient training. This significantly limits the expressive power of S4: its mechanism cannot do content-aware reasoning, it cannot choose which parts of x_t are more important and filter out the rest, and so on.

Gu and Dao (2024) introduce the selective scan algorithm that lets B, C, and Δ (not A, though) depend on x_t while still providing an efficient algorithm for training. In essence, they find a middle ground between the two extremes:

• in RNNs and S4, the state has a (relatively small) fixed size so we cannot fit too much in the hidden state, leading to problems with long-term memory;
• in Transformers, the state is basically the entire sequence, so there is no memorization problem (you have direct access to everything) but lots of problems with processing long sequences (that we have been discussing today and in a previous post);
• the word “selective” in “selective scan” means that Mamba chooses which information to put in a state, with context-dependent mechanisms for putting something into the hidden state and ignoring other parts of the input.

Again, the technical details of the algorithm are too involved for this post—it even makes use of hardware optimization, being specifically tailored for GPUs and TPUs. But the result is the Mamba block that can be stacked in a neural network. It includes the following selective state space model as a replacement for the attention mechanism:

Mamba was big news. A viable alternative to Transformers that even outperformed existing open source language models with an equivalent number of parameters. So it is no wonder that researchers picked up this idea and ran with it, with a lot of papers already extending and improving upon the basic Mamba architecture. 

For example (I’m only listing some of the most interesting ones):

• Mamba was never limited to language modeling; the original paper already applied Mamba to audio processing and modeling genomic sequences; Vision Mamba (ViM; Zhu et al., 2024) is a good representative of how Mamba can be applied to image processing; they show improved results with an architecture very similar to the Vision Transformer (ViT; Dosovitsky et al., 2020) but based on Mamba blocks; another way to process images has been suggested in the VMamba architecture (Liu et al., 2024), which is an interesting combination of CNNs and Mamba;
• U-Mamba (Ma et al., 2024) goes even further and shows that Mamba is not limited to Transformer-like architectures: this is a U-Net-based architecture intended for biomedical image segmentation, and the authors design a CNN-SSM block, a hybrid between convolutions and Mamba, which improves segmentation results;
• among more advanced versions of image segmentation, SegMamba (Xing et al., 2024) considers 3D image segmentation while Video Vision Mamba (ViViM; Yang et al., 2024) does segmentation in video, and MambaMorph (Guo et al., 2024) uses a Mamba-based architecture to establish the correspondence between two important biomedical modalities, MR and CT scans;
• MoE-Mamba (Pioro et al., 2024) adds the mixture of experts (MoE) idea to a Mamba block, leading to a much more efficient architecture; MoE variations of Transformers and other models are a separate can of worms that I plan to open in some future post.

As you can see, the ideas of Mamba have been actively developed by the deep learning community over the last year… actually, no, you don’t see the full extent of it yet. I introduced a hidden constraint here: the original Mamba paper was first published in December 2023, and all the papers cited in the list above are from January 2024! In only a month, Mamba already became a staple of deep learning, and by now, a survey by Qu et al. (2024, last revised in mid-October) has 244 citations—not all of them are Mamba-based models, of course, but it looks like over a hundred, if not more, are Mamba variations published in 2024. 

This is the crazy research landscape we are living in now, and, of course, I cannot give a full survey here, so I will only highlight a direct continuation: Mamba 2 (Dao, Gu, 2024), developed by the authors of the original, dives further into the Mamba algorithm and makes it even more efficient with its state space duality (SSD) framework. It very much looks like Mamba-based models are reliably beating Transformers in many long-context tasks, combining the efficiency of linear attention with the structured adaptability of SSMs.

Conclusion

Linear attention and state space models like Mamba represent a new wave of more efficient models that alleviate the quadratic complexity problem of basic self-attention. These models revisit foundational ideas from RNNs and associative memory but also redefine how we think about integrating memory and content-aware reasoning into neural architectures. They are already pushing the boundaries of scalable and content-aware sequence modeling, and this research direction is far from completely explored.

In this post, we have discussed the basic ideas of linear attention; I have tried to explain the foundations of these models—the kernel trick, associative memory, state space models—that date back a long time. This is another case where recent results can be placed in the context of a machine learning timeline that dates back many decades; here is my take on the timeline of the main ideas we mentioned today:

Once these ideas get picked up in a new form, such as Mamba, progress starts anew, and these days it proceeds at a breakneck pace. I hope that this post gives a clear understanding that this is still very much a work in progress, and new results will probably augment these ideas in the nearest future. Existing results already suggest many exciting applications: not only improved language modeling but also applications to genomics, image processing, audio processing, and more have already been explored in Mamba-like models.

Moreover, we can already look ahead a little. State space models, kernel-based attention, and hardware-aware optimizations in Mamba hint at a future where memory-intensive applications such as long-context language modeling and large-scale genomic analysis are not only feasible but practical. In this future, neural networks may be able to dynamically tailor their computation to the input; perhaps we are witnessing the birth of a new paradigm for sequence modeling.

As research in Mamba and its successors continues, we are also likely to see further breakthroughs in one of the most important issues that still remains to be solved: how can neural networks manage and process memory? In my opinion, memory is still an unresolved challenge; increasing the context size is not the same as having a working memory, but the selective state space models developed in Mamba actually come much closer. I am very excited to see what the next step will be.

Sergey Nikolenko
Head of AI, Synthesis AI

Although deep learning is a very new branch of computer science, foundations of neural networks have been in place since the 1950s: we have been training directed graphs composed of artificial neurons (perceptrons), and each individual neuron has always looked like a linear combination of inputs followed by a nonlinear function like ReLU. In April 2024, a new paradigm emerged: Kolmogorov-Arnold networks (KAN) work on a different theoretical basis and promise not only a better fit for the data but also much improved interpretability and an ability to cross over to symbolic discoveries. In this post, we discuss this paradigm, what the main differences are, and where KAN can get us right now.

Connectionism: the Foundation of Neural Networks

One surprising feature of artificial neural networks is that they basically have not changed since 1943, when Warren McCulloch and Walter Pitts published their seminal paper, “A logical calculus of the ideas immanent in nervous activity”. Already in this paper, before even the Turing test, let alone the Dartmouth seminar (1956) and the first machine learning models, neurons were modeled as linear combinations of inputs with nonlinear activation functions:

This is indeed a very reasonable approximation to what real neurons do, if you try to measure the frequency of spikes as a function of the neuron’s inputs. The function h has to be nonlinear if you want to have a network of neurons, because otherwise the whole network would be a composition of linear functions, so it would be just equivalent to a single neuron.

In the early days of artificial intelligence, the nonlinearity h was usually the threshold function (Heaviside step function for the mathematically inclined): 1 if the input exceeds some threshold a and 0 otherwise. Later, researchers realized that you can’t really train a deep network with threshold activation functions: their derivatives are zero almost everywhere, and gradient descent does not work, so they switched to sigmoidal functions such as the logistic sigmoid and the hyperbolic tangent, which in essence represent “soft” differentiable versions of the threshold. Later yet, ReLU showed that just a little bit of nonlinearity suffices, and by now we also have functions found by automated search such as the Swish (Ramachandran et al., 2017) or its generalization, the ACON family (Ma et al., 2020).

I will not go into more details here. The important thing for us now is that throughout the entire history of neural networks, only the exact form of the nonlinearity has changed. The basic construction of neural networks has remained the same: it is a huge composition of neurons, and each neuron is a linear combination of inputs followed by a nonlinearity. There exist other types of nodes in the computation graph—for example, the batch normalization layer also has trainable weights but it is a different function—but the vast majority of neurons in any modern network look like the picture above. For example, the self-attention layer in a Transformer, which we have discussed previously, does quite a few interesting things with queries, keys, and values, but these vectors are still linear combinations of input embeddings with trainable coefficients.

This idea is known as connectionism: a large network of small simple units can represent very complex things in combination. Philosophically speaking, connectionism makes claims about cognitive processes, saying that our mental phenomena also can arise from a large composition of simple individual neurons. Here, connectionism has been historically at odds with computationalism, which says that the mind works by conducting formal operations on symbols, like an abstract computer (a Turing machine of sorts). There is no direct contradiction between the two—formal operations can be implemented on a large network of units—but there was still an interesting debate left: how would a connectionist theory of mind explain the logical properties of human cognition such as systematic relations in language cognition or compositionality of mental representations? There exist interesting answers to this question, and I will leave a couple of links to book overviews for the interested reader (Bechtel, Abrahamsen, 2002; Marcus, 2003; Maurer, 2021).

We will return to connectionism vs. computationalism later, but, fortunately, we do not have to dive deep into the philosophical or neurobiological aspects of this debate. All that matters to us, lowly computer scientists, are the mathematical and algorithmic sides of the question: what kinds of functions can one represent with compositions of simple ones, which “simple” functions are needed exactly, and how can we find them and the necessary composition?

Universal Approximation Theorems

Neural networks work because even while each neuron is a very simple construction, their compositions can approximate any (continuous) function, with any given precision. Results of this class are known as universal approximation theorems. Specifically for neural networks, several such results were obtained in the late 1980s. In 1988, George Cybenko proved that neural networks with a single hidden layer and sigmoidal activations can approximate any continuous function (Cybenko, 1988). Concurrently with him, Hornik et al. (1989) developed a more general treatment, showing that feedforward networks with one hidden layer can approximate any real-valued continuous function over a compact set, even extending the result to measurable functions. This result was shown for “squashing” activation functions, that is, sigmoids—non-decreasing functions that go from 0 on the left to 1 on the right—but later Hornik (1991) extended it to other classes of activation functions.

Note that these are classical existence results that give a nice reassurance that approximations exist for but do not actually guarantee that you can find it in reasonable time. Moreover, they do not constrain the size of the approximating neural network, and indeed, to approximate a complicated function with a network with a single hidden layer you might need exponentially many neurons.

There exists an entire research direction proving extensions of these results to neural networks with various numbers of neurons, to deeper networks, bounding the approximation errors and so on, with many interesting and beautiful mathematical results. For example:

• Maiorov and Pinkus (1999) constructed a continuous activation function that realizes lower bounds on approximation error for a feedforward network in practice (meaning that they have a construction for this function but it would be, of course, utterly impractical to actually use it);
• Gripenberg (2003) showed that instead of making a single layer wider you can have a bounded number of neurons on each layer and grow the layers to infinity, still getting a universal approximator;
• Lu et al. (2017) showed that there is a whole hierarchy of trade-offs between width and depth: there are classes of functions that can be realized by deep networks but cannot be realized by more shallow networks without an exponential number of neurons;
• Yarotsky (2017) concentrated on networks with ReLU activations and provided specific bounds on their approximation errors, again comparing networks of different depth; in the same vein, Hanin and Sellke (2017) found the minimal width necessary for a deep network to be a universal approximator, again for ReLU activations, and later Shen et al. (2022) proved a series of tight bounds on the approximation rate of ReLU networks;
• Guliyev and Ismailov (2018) constructed a two-layer feedforward network with 3d+2 hidden neurons in total with fixed weights that can approximate any continuous d-variable function with arbitrary precision, and so on, and so forth.

But for today’s topic, instead of going further to recent results and considering the state of the art in universal approximation, we need to take a step back into the 1950s.

Kolmogorov–Arnold representation theorem

Andrey Kolmogorov was one of the most prolific mathematicians of all time, a rival of Euler and Gauss. He introduced the modern axiomatics of probability theory, generalized the law of large numbers, introduced a new notion of an algorithm and founded the theory of Kolmogorov complexity, created chaos theory in the famous Kolmogorov–Arnold–Moser (KAM) theorem, and much more. He revolutionized Soviet mathematical education, establishing some of the best mathematical schools in the world. While sometimes he had to do some questionable things (e.g., participated in the campaign against his former teacher Nikolai Luzin in the 1930s), he actually managed to navigate the Soviet ideological landscape perfectly, never losing his integrity and protecting other people whenever he could (see “The Kolmogorov Option” by Scott Aaronson).

Vladimir Arnold was a pupil of Kolmogorov and a brilliant mathematician in his own right. Compared to Kolmogorov, Arnold gravitated more towards the continuous side of mathematics related to physics, including dynamical systems, stability theory and the above-mentioned KAM theorem, catastrophe theory, fluid dynamics, and much more; in “pure” mathematics Arnold worked in algebraic geometry and topology, also always trying to connect pure mathematics with real world applications. Like his teacher, Arnold was a key figure in Soviet mathematical education, authoring many textbooks and popular texts. He was very annoyed by the formal style of mathematical education originating in the writings of the Bourbaki group, and always advocated for an education that would provide a deeper understanding of the studied phenomena and connect the dots in different fields whenever possible.

Kolmogorov and Arnold collaborated a lot, especially in the early stages of Arnold’s career when he was Kolmogorov’s student. The theorem we are interested in was published in 1957, when Arnold was only 20 years old. It says that any continuous function  of  variables can be represented as the following composition:

   

Here and are arbitrary functions of a single variable, and the theorem says that this is enough: to represent any continuous function, you only need to use sums of univariate functions in a two-layered composition:

This means that if you need to represent a multivariate function of high input dimension, which is what any machine learning model is doing, it would be sufficient to find several functions of one variable. The only multivariate function you need is the sum, the rest can be pushed to univariate components. 

If you think about it in terms of learning the functions, it means that the Kolmogorov–Arnold theorem gives a way around the curse of dimensionality, the reason why machine learning is hard and often counterintuitive. In low dimensions, every machine learning problem is easy: you can take any integral numerically, nearest neighbors are indeed close by and relevant, you can cover a reasonably sized part of the space with samples from the uniform or normal distribution—everything works great. In high dimensions, volumes grow exponentially, nearest neighbors grow apart, and integrals become impossible to find with any reasonable accuracy; this is exactly the reason why machine learning needs strong assumptions and complicated methods such as MCMC sampling. The term dates back to Richard Bellman (1957) who noted that dynamic programming also becomes very computationally hard in high dimensions; for a more detailed discussion of the curse of dimensionality, see, e.g., Marimont and Shapiro (1979) and Beyer et al. (1999).

Moreover, the theorem also gives you the exact number of functions in each sum: the summation limits and refer to the same n which is the dimension of

*** QuickLaTeX cannot compile formula:
\mathbf{x]

*** Error message:
File ended while scanning use of \select@group.
Emergency stop.

. Compare this to exponential bounds on the number of neurons with sigmoidal activations that we mentioned earlier, and the Kolmogorov–Arnold theorem begins to sound quite tempting to use in machine learning, right? Unfortunately, the theorem itself does not give you any idea of how to find the functions and ; we will discuss this problem in the next section.

I will close this section with another interesting mathematical tidbit. As you have probably heard, in 1900 David Hilbert, a great mathematician and a founder of mathematical logic, compiled a list of 23 so-called Hilbert’s problems. They were unsolved problems that Hilbert believed to be important for the development of mathematics, and his intuition was completely right: although some problems turned out to be either relatively easy or too vague to judge, many of them led to the development of entire new fields of mathematics. One of the still standing Hilbert’s problems, proving Riemann’s hypothesis, also made the list of the Millenium Prize Problems by the Clay Mathematics Institute, an update on Hilbert’s idea for the new century.

As it turns out, the Kolmogorov–Arnold representation theorem arguably solves one of Hilbert’s problems, namely the thirteenth problem. It was already known to Hilbert that any seventh-degree equation can be reduced to the form

   

It seemed to be impossible to reduce this equation further, so it was a tempting hypothesis for Hilbert that the seventh-degree equation gives you an irreducible algebraic function, in the sense that you cannot reduce it to a superposition of functions of fewer variables. The Hilbert’s Thirteenth Problem is thus as follows:

Consider a seventh-degree equation in the reduced form as above. Its solution is a function of three variables: the coefficients a, b, and c. Can it be expressed as a composition of a finite number of two-variable functions?

This problem was originally posed for algebraic functions, i.e., functions that can be defined as a root of a polynomial equation, but later Hilbert asked a version of this problem about arbitrary continuous functions. Kolmogorov and Arnold were actually working on this problem, and they solved it in several steps, gradually reducing the number of variables required for elementary functions: first Kolmogorov showed that any continuous function can be represented as a composition of function of three variables, then his student Arnold reduced it to two (already solving Hilbert’s problem), and then came their main theorem.

For the continuous version of Hilbert’s Thirteenth, the Kolmogorov–Arnold representation theorem is actually an overkill: it turns out that we only need arbitrary continuous functions of one variable and addition, which is technically a two-variable function. Note, however, that the algebraic version still remains unsolved: Arnold himself returned to it later with Goro Shimura (in the proceedings of a 1976 symposium on the legacy of Hilbert’s problems), but the efforts of mathematicians have not been successful so far (Vitushkin, 2004).

From an Existence Proof to Practical Algorithms: Splines

As we have seen above, the Kolmogorov–Arnold representation theorem is purely existential; the original result does not give you a good way to find the univariate functions. There have been several attempts to give a constructive proof that would provide an algorithm for finding these functions (Sprecher, 1965; Sprecher, 1972; Braun, Griebel, 2009), but these attempts were hardly practical from a machine learning standpoint. 

Moreover, there have been negative results showing that univariate functions in the theorem can be very complex, even fractal, and learning them can be very hard; one of these results even says “Kolmogorov’s theorem is irrelevant” right in the title (Girosi, Poggio, 1989). So how could the KAN approach find univariate functions in the Kolmogorov-Arnold representation efficiently?

There have been earlier approaches to build neural networks based on the Kolmogorov–Arnold representation theorem. Hecht-Nielsen (1987) and Lin and Unbehauen (1993) noted that the theorem, specifically in its constructive form by Sprecher (1965), leads to natural constructions of three-layer neural networks; see also (Sprecher, Draghici, 2002). Köppen (2002) developed an algorithm for learning the Sprecher representation. 

However, these algorithms remained impractical for two reasons: first, because learning the univariate functions was still too hard, and second, because the shallow three-layer architecture required special algorithms to train and could not be trained by simple gradient descent. Let us begin with the first constraint.

To make univariate functions easier to learn, various approaches to making the Kolmogorov–Arnold representation theorem practical centered on splines. Splines (Bartels et al., 1995; Shumaker, 2015) are piecewise polynomial functions used to approximate or interpolate other functions. The key idea is that instead of using a single complex function to fit all data across the entire domain, a spline breaks the domain into smaller intervals and fits a much simpler function (usually a low-degree polynomial) to each interval. These polynomial pieces are smoothly connected at certain points called knots.

If we use splines for univariate polynomial regression, formally it means that we consider the interval where the data points lie and break it down with intermediate points , the knots, getting  intervals:

   

The task is to find a polynomial  of degree  on each interval, , so that:

• the entire collection of polynomials minimizes some loss function for the data, usually the sum of squared residuals for all data points :

     

• the polynomials come together smoothly, with their values and derivatives matching at the intermediate knot points; usually a spline of degree  would require all derivatives up to the -th to match: for all  from to , 

     

The main difference between splines and just piecewise interpolation lies in this last condition: splines impose additional constraints to make the connections continuous and even smooth. For example, if I plot three segments of data and try to learn quadratic or cubic regression on each, the results will follow the data but it will be three independent discontinuous curves (thin curves in the plot below). A spline regression would make the curves meet each other in the knots, and, moreover, meet each other smoothly, with matching derivatives (thick curves in the plots below):

There is a rich field of applied mathematics on splines; they are often used for interpolation, i.e., to make a smooth curve that goes near all given points rather than approximating a least squares polynomial regression. The splines shown above are actually learned linear combinations of B-splines, i.e., polynomials that can serve as basis functions for splines of a given degree; there exist algorithms to compute B-splines for a given degree and knot points (Gordon, Riesenfeld, 1974; de Boor, 1977; Lee, 1982); these algorithms, in particular the de Boor–Cox iteration (de Boor, 1972; Cox, 1972), are relatively efficient but become computationally hard for large numbers of knots, and we will return to this discussion later. This is also adjacent to the discussion of Bezier curves that are a special case of B-splines. I will not go into more details about splines and will refer to the numerous existing books and material on the subject (Bartels et al., 1995; Gallier, 1999; Shumaker, 2015; Hovey, 2022).

Splines provide a natural algorithm to learn smooth functions in a very expressive way; by changing the degree and number of knots we can freely change the number of parameters in a polynomial spline, from a piecewise linear function up to literally an interpolation polynomial for the data points. However, splines become much harder to use in high dimensions, so it would not be a good idea to replace regression models with splines. But the Kolmogorov-Arnold theorem removes the need for high dimensions altogether! Therefore, it is no wonder that splines caught the attention of researchers looking for efficient univariate functions to use in the Kolmogorov-Arnold representation.

Leni et al. (2013) developed what was called a Kolmogorov spline network. Fakhoury et al. (2022) presented ExSpliNet, a neural network architecture based on B-splines. An even more interesting direction would be to change activation functions into learnable splines: after all, ReLU is just a linear spline with two components. Campolucci et al. (1996) and Guarneri et al. (1999) explored this idea back in the 1990s, and they were already building upon Jerome Friedman’s adaptive spline networks (Friedman, 1991). More recently, this approach has been developed by Scardapane et al. (2018) and Bohra et al. (2020).

But somehow, these ideas have not made any splash in the deep learning world before very recently. Kolmogorov–Arnold networks also use learnable activation functions based on splines. What is the difference here, what are the new ideas, and why have KAN attracted significant attention in 2024?

Kolmogorov–Arnold networks

The first KAN paper (Liu et al., 2024) begins with a natural question: “are multilayer perceptrons the best nonlinear regressors we can build?” They begin by comparing the Kolmogorov–Arnold representation with usual multilayer perceptrons and note that they can make the former deeper and/or wider than the theorem suggests, which may help make individual univariate functions simpler. Here is the teaser image by Liu et al. (2024) that makes this comparison:

They define a “KAN layer” with inputs and  outputs as an  matrix of one-dimensional functions with trainable parameters: the –th output is the sum of the results of the  functions in the corresponding row. The original Kolmogorov–Arnold representation consists of two such layers: first,  inputs turn into outputs via functions, and then combine intermediate values into a single output. When you look at the representation like this, it becomes clear how to stack more such layers, making a deeper KAN that represents a composition of such matrices of functions:

   

This is a very general representation; for example, a feedforward neural network (a multilayer perceptron) can also be represented as a KAN with linear functions (weight matrices) interleaved with activation functions (applied componentwise, so in the notation above it would be a diagonal matrix of functions):

   

On each KAN layer, every transformation function ɸ is introduced by Liu et al. (2024) as a weighted sum of a basis function b and a spline function s,

   

where  is the sigmoid linear unit (SiLU) activation function and  is a B-spline:

   

As a result, every KAN layer has parameters, where is the number of inputs and outputs, is the degree of the spline, and  is the number of knots. Liu et al. (2024) discuss a lot of design choices and other aspects of KANs but at this point, let us proceed to an example, which I adapted from this tutorial.

Let us begin with a nontrivial function that we want to approximate by a KAN; let’s take one of the functions used in the original paper:

   

To get a feeling for what this function looks like, the figure below shows the heatmap for f(x, y) and several one-dimensional slices of this function in both directions:

To train a KAN for this function, first we need to set up its structure; let’s mimic the structure of the function and set up a [2, 2, 1] KAN, i.e., a composition of the form

   

After training, we get a rather small loss on the test set (produced by the same function), and the following learned functions:

As you can see, indeed resembles a sinusoidal function, and looks suspiciously quadratic. Even at this point, we see that KAN not only can train good approximations to complicated functions but can also provide readily interpretable results: we can simply look at what kinds of functions have been trained inside the composition and have a pretty good idea of what kinds of features are being extracted.

But we can do even better. Suppose that by looking on these plots, we have noticed that is very similar to the quadratic function  (actually, in this case, but the minus sign is best left for the linear combination). KAN allows us to substitute our guess symbolically into , fixing it to be and training the rest of the functions. If we do that, we get a much better test set error, will still look sinusoidal, and, most importantly, the resulting will look much more like the exponent that it is in the original:

So by now, we can also correctly infer the other functions in the composition. Doing this kind of symbolic reasoning requires an iterative process of looking at the functions and substituting some of them symbolically, but it still beats trying to analyze a multilayer perceptron by a very large margin. In practice, we will not know the correct form of the KAN composition but one can start with a larger KAN and reduce it, looking at what happens with the approximation error.

Liu et al. (2024) suggested that this could be helpful for deriving complex dependencies in physics or applied math, when you need to explain experimental data with a formula; they show several interesting examples related to learning symbolic formulas for quantum physics (to be honest, I am very, very far from an expert on quantum physics so I will not attempt to explain the physics part here). They called KAN “a language model for AI + Science” and even provided a decision tree for choosing between KANs and regular MLPs in applications:

In other words, KANs were suggested as helper models for semi-automated learning in science and generally situations when you would like to obtain a symbolic formula as a result.

Making KANs Efficient: FastKAN and ReLU-KAN

The original paper by Liu et al. (2024) was posted on arXiv on April 30, 2024. It was immediately noticed and received some coverage but the initial impression was that KAN applications are very limited due to their high computational complexity. The problem is that in order to construct B-splines of degree 3 that KANs are based on, you have to run the above-mentioned de Boor–Cox iteration that becomes a significant computational bottleneck for KAN, especially rescaling the spline grids.

In less than two weeks, on May 10, 2024, Ziyao Li uploaded a three-page preprint to arXiv where he introduced FastKAN, a method that achieves equivalent results while having about 3x faster forward propagation. His idea is that B-splines are basically equivalent to Gaussian radial basis functions (RBF), a traditional way to extract local features in machine learning. Training a one-dimensional linear regression with RBF means that you are learning the weights a linear combination of features each of which depends on the distance between x and its center μ_i, with Gaussian RBFs having exponential decay around μ_i similar to the normal distribution:

   

Li (May 2024) showed that you can replace B-splines with Gaussian RBF functions and achieve significant performance improvements with basically no difference in the results. With this simple alteration, KANs suddenly became much more practical—another wonderful example of low-hanging fruit that one can find in deep learning even now (although nowadays you really have to be quick about it).

But that’s not the end of the story, of course. Another two weeks later, on June 4, 2024, Qiu et al. published a more detailed arXiv preprint that tried to alleviate the very same restriction. They replaced the B-spline basis functions with a new function composed of ReLU activations, specifically

   

Here and are trainable parameters, which makes a rather diverse family of functions, and is the regular ReLU activation function; here is an illustration by Qiu et al. (2024):

The main advantage of these basis functions is that they can be expressed via matrix operations such as matrix addition, dot products, and ReLU activation. This makes them much faster in practice than KANs based on B-splines; the authors report 5-20x improvements in training speed while also significantly improving the fitting accuracy.

So one month after the original paper on KANs, we already had two much more efficient versions that could be scaled further than a regular KAN and applied much wider. These were the papers that started the hype. Half a year later, where are we with KANs now?

Recent developments in KAN: Architectures

In any field of science, you expect that a new idea that can open up a new field of study will be gradually developed afterwards; at first, the authors of the model will try to milk it for new results, then other researchers will see the potential and join in, and if the idea is good, ultimately a subfield will arise. The main difference between mostly any other field of science and deep learning is that while in “regular” computer science this process would take at least a few years, in deep learning it has already happened in several months. The original paper by Liu et al. (2024), posted on arXiv in April 2024, by mid-October has already over 250 citations (Google Scholar), and a curated list of links about KANs notes over a hundred interesting papers and resources that directly continue this research. So while in June 2024 a comprehensive survey of KANs was possible (Hou, Zhang, 2024), now, just half a year after the original publication, it is already basically futile to try and review everything people have done in this direction; below, I will survey a few papers that look most interesting to me.

Let us begin with improved architectures; I will note two works in more detail and give a brief survey of several others.

Bodner et al. (June 2024) were the first to introduce Convolutional KANs, an architecture that combines the KAN approach with convolutional networks. But here I want to highlight the work by Yu et al. (October 2024) who introduce a special kind of Chebyshev polynomial-based KAN convolutions (see also Sidharth, Gokul, May 2024), which is a reformulation of KANs designed to extract features from patches of the input tensor, just like a CNN:

Then Yu et al. start off with traditional convolutional architectures and add layers of these new convolutions with residual connections around classical CNN layers such as ResNet (left) or DenseNet (right):

The resulting architectures, called Residual KAN (RKAN), shows performance improvements on classical datasets; the authors especially note that RKAN’s performance benefits grow with the complexity of the dataset and model size, suggesting that such feature extraction units can be beneficially added to many different architectures.

Yang and Wang (September 2024) present the Kolmogorov–Arnold Transformer (KAT), a model that replaces MLP layers in transformers with Kolmogorov-Arnold Network (KAN) layers. Their main applications lie in computer vision tasks, so their teaser image shows ImageNet accuracy and compares KAT with ViT-like models:

The idea is that while KANs are known for their parameter efficiency and can learn powerful and concise representations, it is challenging to integrate KANs into large-scale models such as the Transformer. The paper lists three core problems:

• inefficiency of B-spline functions in computations on GPUs,
• exponential growth of parameters in KANs, and
• difficulties in initializing KAN weights for convergence in deep networks.

To address these issues, KAT introduces respectively three key innovations:

• rational activation functions that replace B-splines with rational functions, which are better suited for modern hardware and allow for an efficient CUDA implementation,
• Group KAN, where activation weights are shared across groups of neurons, reducing the number of parameters and computational load, and
• variance-preserving initialization, an approach that initializes activation weights so that variance in activations remains the same across layers.

As a result, KAT can successfully integrate KANs into Transformers and achieves several state of the art results in vision tasks, including image recognition, object detection, and semantic segmentation, where KAT outperforms traditional Transformers with MLP layers. For example, on the ImageNet-1K dataset the KAT model exceeded the accuracy of a ViT model of the same size by 3.1%, which is no small feat given that the overall accuracy is already at 82%. Performance improved even further when KAT was initialized with pretrained ViT weights.

Among other news in KANs, let us note the following:

• Recurrent KANs (RKAN) and Temporal KANs (TKAN: Genet, Inrizillo, May 2024) apply KANs to time series data by developing recurrent architectures with the KAN approach; RKAN are parallel to standard RNNs, and TKAN is an adaptation of LSTM to KANs;
• GraphKAN (Zhang, Zhang, June 2024) inserts KANs into graph neural networks (GNN), also reporting improved feature extraction performance;
• UKAN (Li et al., June 2024) introduces KANs into the classical U-Net architecture that has been widely used in computer vision, specifically in image segmentation;
• DropKAN (Altarabichi, July 2024) is a special form of dropout that is shown to improve KANs;
• Higher-order-ReLU-KANs (HRKANs; So, Yung, September 2024) extend the ReLU-KAN method, which is based on a square of a ReLU activation, to higher degrees of ReLU activations, showing improved performance;
• and many more interesting developments have not yet been followed up much but may open new possibilities for research, including Gaussian Process KAN (GP-KAN; Chen, July 2024), Rational KANs based on rational functions (Aghaei, June 2024), and Fourier KANs where learnable activations are modeled as Fourier series (Mehrabian et al., September 2024).

However, various KAN-based architectures are just a means to an end; what have the ends been, i.e., how have KANs been used in practice?

Recent developments in KAN: Applications

We have noted above that the original KAN were developed in part with scientific applications in mind: KANs can yield symbolic results and explain their predictions with compact and readily interpretable formulas.

The next step in this direction was taken by the KAN 2.0 approach developed by Liu et al. (August 2024). The goal of KAN 2.0 is to create a two-way synergy between KANs and scientific knowledge, both embedding prior scientific knowledge into KANs and extracting new scientific insights from them:

Architecturally, the authors make several interesting contributions:

• a variant of KAN called MultKAN that includes additional multiplication nodes in KAN layers, enhancing the network’s ability to model physical processes that involve multiplicative relations; standard KANs would be hard pressed to approximate , while MultKAN would do it with a single multiplication node;
• KAN Compiler (kanpiler), a tool that converts symbolic formulas into KAN structures by parsing them into tree structures and inserting the trees into the network directly; this tool is responsible for much of the left-to-right arrow in the diagram above, allowing to incorporate prior symbolic knowledge into the network; the authors also develop the opposite tool, tree converter, to convert KANs into tree graphs;
• revealing modular structures, i.e., enforcing tighly connected modular structures within KANs while minimizing inter-module connections, which helps capture the often separabile and symmetrical scientific models.

As a result, Liu et al. (2024) show how KANs can be applied to discover and interpret physical laws, including:

• Identifying conserved quantities in physical systems, such as energy and angular momentum in a harmonic oscillator;
• Lagrangians, where KANs are trained to approximate the Lagrangian for simple mechanical systems such as a single pendulum or relativistic mass in a field;
• discovering hidden symmetries, with the example of semi-automatically discovering translational invariance in the Schwarzschild black hole metric that took 17 years for physicists (Painlevé and Gullstrand) to discover in the 1920s.

This still looks like the most direct practical application of KANs: their direct relation to symbolic formulas, with easy conversions back and forth, may lead to important discoveries.

However, this is not the only application. Models that I mentioned in the previous section all come with convincing practical results where KAN-based architectures outperform similar architectures without KANs. Let me note a few more interesting papers that introduce new applications of KANs:

• Nagai and Okumura (July 2024) integrate KANs into molecular dynamics (MD) simulations to improve the accuracy and efficiency of interatomic potentials; in modern MD simulations, these potentials are commonly modeled by neural networks, and the authors note that KANs result in a significant reduction in computational costs compared to potentials based on classical neural networks: KANs can approximate potential energy surfaces with a simpler representation without sacrificing accuracy;
• Ge et al. (August 2024) present TC-KANRecon, a KAN-based approach for magnetic resonance imaging (MRI) reconstruction; they adopt KANs to strike a better balance between image denoising and structure preservation, and produce improved reconstructions within a given computational budget;
• Aghaei (September 2024) leverages KANs to solve optimal control problems; his KANtrol framework is an adaptation of the well-known approach of physics-informed neural networks (Raissi et al., 2019) which embed prior physical knowledge into neural networks; this work shows that, unsurprisingly for us by now, KANs handle this prior knowledge better and produce better approximations to both the control functions and state evolution in optimal control problems;
• GNN-SKAN (Li et al., August 2024) a novel approach integrating Kolmogorov-Arnold Networks (KANs) with Graph Neural Networks (GNNs) specifically to improve representation learning for molecular graphs; the authors develop a special variant of KANs called SwallowKAN (SKAN) for this and show better generalization performance to diverse classes of molecular structures.

As you can see, most of these applications still center on using KANs for science, inferring mathematical dependencies from data in various domains; time will tell if preliminary promising results in other directions such as image processing convert to practical models.

Conclusion

I originally thought this post would be relatively short; Kolmogorov–Arnold networks seemed like an interesting idea that would make for a good case study of “something completely different” in the field of deep learning that might or might not lead to good results in the future. However, as I fell deeper and deeper into the rabbit hole of KANs, they seemed more and more promising, so this post had gradually turned into a full-sized review.

I cannot but imagine how interesting it would be to pair KANs with an advanced LLM that might try to automatically notice what functions are being learned. An LLM will tirelessly try different approaches in what seems to be a perfect match for their capacity for creative data analysis without too much intermediate logical reasoning. The o1 family of models already looks like a very promising candidate for this LLM (see my post on o1-preview), and the models will only get better from here.

But Kolmogorov–Arnold networks still do make for an excellent case study. Based on an idea that had been around forever, KANs were introduced at the end of April 2024. It is October now, and KANs have already blossomed into a well-developed research direction, with dozens of papers introducing new directions and applications. In this post, I have tried to give a brief overview of this direction, and I believe it is an interesting one, but my main point is that this is but one of many possible ideas worth exploring. I am sure that deep learning has many more such ideas in store, waiting for researchers to discover them; good luck!

Sergey Nikolenko
Head of AI, Synthesis AI

OpenAI’s o1-preview has been all the buzz lately. While this model is based on the GPT-4o general architecture, it boasts much improved reasoning capabilities: it can ponder the question for about a minute, reason through multiple possibilities, and arrive at solutions that could not be generated from a single try of GPT-4o. In this post, I discuss the o1-preview model but mainly present the most striking advantage of o1-preview over all previous LLMs: it can meaningfully answer questions from a quiz game called “What? Where? When?”. At this point, it probably does not sound all that exciting compared to winning math competitions and answering PhD level questions on science, but let me elaborate.

“What? Where? When?”: a Game of Trick Questions

There have already been many responses to OpenAI’s o1-preview, and this post is also one of them. We will discuss the model and what new opportunities it offers below. But first and foremost, this is a post of love for a game called “What? Where? When?” (“Что? Где? Когда?”), usually abbreviated to ЧГК in Russian; I don’t expect the English acronym WWW to catch on but I’ll stick to it throughout this post for brevity.

The rules are simple: teams of at most six players are answering questions. The question is read for all teams, they are given one minute to discuss and arrive at the answer. During the discussion, access to the Web or other reference material is not allowed. At the end of a minute, the teams are given another 10 seconds to write down their answer on a piece of paper, the answers are collected, and the correct answer is announced. The team that has answered the most questions correctly wins. I’ve made an illustration just in case, but the rules are really very, very simple:

What differentiates WWW from just about every other pub quiz in existence is the style of questions. Here is one (to avoid authorship issues, all examples are questions that I personally wrote, usually at some point between 2005 and 2015 when I was actively preparing questions for the game):

The Sunday Times wrote about this person, born in the 1930s, that his work represents a ceiling for wide audiences, even though in principle no one is stopping you from consuming more elite art. Write the last name of this person.

Naturally, you are not supposed to know what The Sunday Times wrote at some unspecified point of time. Instead, the question is supposed to draw on your general knowledge but also require nontrivial logical and intuitive jumps to arrive at the answer. At the same time, the answer should be unique and no other answer should fit the question; appeals are allowed for cases when this principle is violated, because the question’s author sometimes cannot think of every possible alternative.

Try thinking about the question above by yourself for a little while before reading on. What are your thoughts?

A seasoned WWW player could reason through this question somewhat like the following:

• the question directly tells us the following facts:
  • the guy in question (it’s a guy because of the “his” pronoun) worked on some kind of art;
  • his art is elite but not too elite to be incomprehensible so he is relatively well known to wide audiences;
  • he was born in the 1930s so his best work was probably done at some time between the 1960s and 1990s; he might be alive now (though very old);
• based on this, you could propose some hypotheses, but, of course, this information is insufficient to single out one person (e.g., David Hockney fits quite well) so we need to consider indirect clues:
  • what parts of the question could constitute hints?
  • there is one candidate, the word “ceiling”; the question goes out of its way to mention this word, it’s not the most natural word for the context, and the actual information content would not change if it didn’t mention “a ceiling for wide audiences” at all, so the word itself must be important;
• now comes the intuitive jump that you have to make:
  • combine the word “ceiling” and actual information that his art represents this ceiling although “more elite art” is also technically available to everyone;
  • how would you describe a situation like this, where a person stops at some point although technically there is no barrier to go further? maybe in a different context?
  • the jump is that you could describe this situation as a “glass ceiling”, a phrase that usually relates to advancement opportunities for oppressed demographics but whose meaning also fits the situation in this question;
• when you arrive at the phrase “glass ceiling”, you already have the answer; it only remains to note that Glass is also the last name of a famous composer; finally, you can verify that:
  • Philip Glass is indeed an elite composer whose work is nevertheless widely known and popular, so he fits the facts;
  • you probably don’t know for sure that he was born in the 1930s but it also fits your general knowledge about him; in WWW, dates usually provide general context for the question, e.g., in the musical arts you could be sure it’s not Beethoven or Kanye West but you probably wouldn’t exclude John Lennon (born 1940) or Ennio Morricone (born 1928) because you wouldn’t know their exact birth years;
  • another confirmation lies in the fact that the question specifically asks for the last name rather than just asking to name the person, and the last name is what is used in the key phrase; it could be a coincidence but it also could be a weak hint;
• and indeed, Philip Glass is the correct answer.

As you can see, this is definitely not direct trivia. When you think about a WWW question, you have to make a lot of assumptions and jumps that are not directly supported by either facts or logic. An important skill is to reason backwards from the question: why it is phrased in the exact way that it is, what the author has been trying to convey; in the example above, this reasoning singles out the word “ceiling”.

In this post, I’m describing the “competitive” version of the game, where multiple teams compete against each other, but I have to note that it originated from a Russian TV show called What? Where? When? where a single team of six players answers questions sent in by the viewers (naturally, the questions are selected and edited in advance, otherwise it wouldn’t be a fun game at all). This is literally the longest running show on Russian television, originally airing in 1975 and not changing too much since then. In 2010, ABC licensed What? Where? When? under the name Million Dollar Mind Game, and while they did a good job capturing the style of questions and the spirit of the game (you can find the show on YouTube, in 360p quality alas), it didn’t take in the U.S. and was canceled after a season or two.

Can AI Models Play “What? Where? When?”: The Surprising Development of o1-preview

I have been playing WWW for… God, how time flies, for 25 years already. To me, this is a perfect hobby because while it is competitive, it not only never gets boring itself—questions never repeat—but also does not involve any boring preparation bits that basically any other sport would. Scrabble tournaments make you memorize dictionaries (in a famous case, Nigel Richards won the French-language Scrabble World Championships without any knowledge of the language!), and Jeopardy pros learn a huge amount of trivia, but here, while a high level of general knowledge is required, you mostly learn it by osmosis through playing the game itself. Simply memorizing a lot of facts won’t get you very far in the game.

Ever since I started working in machine learning and natural language processing specifically—another “time flies” moment, that was almost 15 years ago—I have been testing whether ML models could be any good in WWW. Naturally, they never could. There was absolutely no way an NLP model of the 2010s would actually understand what’s required in a question. You can google the answer fairly often because WWW is mostly a game based on real facts about the real world; in the example above, the “ceiling for wide audiences sunday times” Google query gives me the correct answer at #2 in the list. But even if you gave models access to the Internet, there was no way models would understand what to google for and how to extract the correct answer from retrieval results. This was just way, way above the capabilities of AI models of the time, it always looked like something from a very distant future.

When LLMs came about, I also tried to ask them questions like the above. And they also inevitably failed. LLMs know a lot of facts, and some of them can google behind the scenes (recall our post on RAG), so sometimes they would answer a question simply because they knew the factual answer. But none showed any capability to actually play the game; even a month ago, WWW looked like it would be possible only some relatively long time in the future.

Well, the future is here now. OpenAI’s new model, o1-preview, can play WWW. Moreover, o1-preview can show you its chain of reasoning. So here is how it reasoned through the question above in 44 seconds (under a minute, although I don’t know how to limit its thinking time right now): 

Identifying key characteristics  I’m focusing on a person born in the 1930s, whose work is described as a ceiling for wide audiences, yet not preventing the consumption of more elite art. The task is to find this individual’s last name. Unraveling clues I’m digging into a quiz clue, parsing it creatively to identify a person from the 1930s whose work represents a broad artistic ceiling, hinting at “glass ceiling” or the “Sistine Chapel ceiling” as potential leads for further exploration. Piecing together I’m gathering info on Philip Glass, examining connections to “Glass Ceiling” and the Heisenberg Uncertainty Principle. Considering his work’s accessibility and its metaphorical implications. Weighing possibilities I’m gathering clues about an artist from the 1930s with mainstream appeal. Considering the “no one is stopping you” phrase and connections like “Glass Ceiling,” “Glass,” or “Peter Max.” Analyzing the phrase Considering various interpretations like physical barriers, metaphors for invisible obstacles, and literal elements of ceilings or artists named “Ceiling”. Revisiting artists and interpretations I’m brainstorming artists and interpretations, considering Michelangelo’s Sistine Chapel, the movie “Glass Ceiling,” the Beatles, and “Ceiling Cat.” Pondering cultural icons I’m reflecting on cultural icons like Andre Rieu and the “Mona Lisa,” considering how they might symbolize the pinnacle of mainstream audience art. Weighing the details I’m thinking through the idea that the person’s work, while accessible to wide audiences, may still hold a glimmer of something more exclusive, hinting at a deeper connection or higher tier. Weighing options I’m noticing the possibilities involve John Williams, Andy Warhol, Frank Lloyd Wright, Norman Rockwell, or James Cameron, among others, by examining birth years and the “ceiling” clue.

Examining possibilities I’m thinking through the clue “No one is stopping you from consuming more elite art,” which might imply a barrier or wall. It’s worth considering artists like Glass or Wall, or even the term “Ceiling” to explore. Weighing choices I’m mapping out notable artists born in the 1930s, like Philip Glass and Yoko Ono, and considering the Japanese word for roof, “Ten.” Adjusting my approach Thinking through artists like Richard Serra and John Cage, but considering the phrase “No one is stopping you in principle from consuming more elite art”? Evaluating limits and creators Thinking about “Glass Ceiling” and its connotations with limits and barriers, I’m considering artists, authors, and cultural references, especially those born in the 1930s, to identify the intended creator. Piecing together clues I’m considering artists or figures whose work defines a cultural peak, possibly “Block” or “Lid” in their names. The moon angle hints at Neil Armstrong, born in 1930. Piecing together I’m examining various artists and subjects, like Carl Sagan and Robert Smithson, to understand the clue’s connection to “ceiling” and “Space.” Connecting concepts It’s interesting to see how principles like the Principle of Uncertainty or ideas like Superconductivity might align with the clue, though they seem less likely for now. Weighing possibilities OK, let me see. I’m thinking about whether the clues point to Murdoch or Brecht, considering Rupert Murdoch’s birth and his connection to media, or Brecht’s fourth wall concept. Weighing possibilities I’m mapping out an artist connected to the 1930s or an uncertainty principle, considering figures like “Heisenberg” or others associated with paradoxes. Piecing together musical influences I’m gathering info on Philip Glass, whose minimalist compositions have a broad appeal yet maintain an elite essence. This aligns with the idea of a “Glass Ceiling” in art.

Note how although the model has arrived at the correct answer fairly quickly, it has also generated a lot of interesting and creative possibilities, including:

• a list of suitable artists; John Williams, Andy Warhol, Frank Lloyd Wright, Norman Rockwell, and James Cameron all sound plausible to me except for Rockwell who was definitely born earlier than 1930s—by the way, this suggests that o1-preview was not googling anything;
• a slightly different angle for the “no one is stopping you” hint, in that it “might imply a barrier or wall”; it even linked the hint to the “fourth wall” concept which is also a salient concept often appearing in WWW questions;
• completely different directions that could be promising, such as translating the key words to Japanese.

This is exactly how a good player would try to approach this question, and this is exactly what all models so far, including GPT-4o, the direct predecessor of o1-preview, are failing at. I asked GPT-4o the question above, regenerating the answer several times; while it was clear from its explanations that GPT-4o did understand the question, the answers I obtained were Alfred Hitchcock, Walt Disney, Andy Warhol, and Stanley Kubrick. GPT-4o definitely “knew” that Disney and Hitchcock had both been born much earlier than the 1930s but still gave these answers, with the most popular answer being Alfred Hitchcock (5 times out of 8); several times, GPT-4o explicitly wrote that Hitchcock was born in 1899 but still gave this answer.

So what’s so special about o1-preview? Let’s try to find out.

Reasoning during Inference: A New Scaling Law?

As usual with modern state of the art LLMs, there is little information explicitly given by OpenAI about the structure of its o1-preview model or its training regime. This is natural from the commercial point of view and probably a good thing from the security point of view (recall our post on the dangers of AI), but the net result is that we, like all outside experts, are mostly reduced to guesswork, with the only definitive sources being OpenAI’s announcement post and the OpenAI o1 System Card, which is safety-oriented and does not provide further information about the model itself.

The post vaguely gestures at being better at chain of thought reasoning. I hope to roll out a detailed post on chain of thought techniques in the near future, but, alas, so far it doesn’t look like the o1 family will meaningfully contribute to the scientific part of it. In the quote below, the only load-bearing words are “reinforcement learning”:

Through reinforcement learning, o1 learns to hone its chain of thought and refine the strategies it uses. It learns to recognize and correct its mistakes. It learns to break down tricky steps into simpler ones. It learns to try a different approach when the current one isn’t working. This process dramatically improves the model’s ability to reason.

I don’t have a personal opinion on what exactly this reinforcement learning method is. It could be RLHF applied to chains of internal reasoning. Or it could be something more involved. For example, Subbarao Kambhampati offers a very interesting speculation; he suggests that the o1 family learns to reason in a way similar to how AlphaZero learns to play board games, with text continuations playing the role of moves and “game results” being correct answers as evaluated by external LLMs. For a collection of this and other speculations, see an excellent (as always) survey post by Zvi Mowshowitz.

Whatever the details, the result is that o1-preview introduces a whole new paradigm to large language models. We have discussed many times (here and here, for instance) that LLMs are token prediction machines: they take in as much context as they can (again, see my previous post on context) and then produce the output token by token, autoregressively, never looking back.

The o1 family are still LLMs, but they produce many different outputs, check out different possibilities, combine the results, and generally “think through” the problem. This idea is not novel in itself—it is exactly the premise of chain of thought techniques. But OpenAI could make it work on an unprecedented scale. Look at the plot with the scaling law they report; the Y-axis shows the USA Math Olympiad (AIME) results and the X-axes are two different computational budgets:

The plot on the left is standard: more train-time computation leads to better performance with a log-linear dependency. But the plot on the right is completely novel: it shows that o1 models can actually make good use of test-time (inference) computational resources! Basically, it means that the longer you allow an o1 model to think about a problem, the better it does; I don’t think a scaling plot like that has ever been achieved before with LLMs.

Naturally, this leads to increased costs; as you probably have already noticed, o1-preview comes with some rather strict constraints on usage and steep prices for API access. But costs have a tendency to decrease over time due to algorithmic improvements and cheaper hardware, while peak performance, once achieved, stays with us forever.

And the performance jumps are very impressive. I mostly devote this post to WWW since this is my personal example where I can add something new to the discussion, but answering trick questions is definitely not the most productive use of o1-preview’s computational resources. Here is the performance comparison reported by OpenAI:

In all three cases, o1 blows GPT-4o out of the water. GPT-4o could solve some high-level mathematical Olympiad problems but o1 makes it to the Olympiad, scoring among top 500 participants in the US this year. I’d love to see Claude Opus and Gemini 1.5 Pro on this plot since they are better at math than GPT-4o, but I don’t believe they would be as competitive. Coding has much improved, with o1 breezing through advanced competitive coding problems. Finally, the GPQA Diamond dataset (Rein et al., 2023) is not a high school science test; it contains questions that human Ph.D. students in the corresponding fields tend to answer with 65-75% accuracy when given full access to Google and over 30 minutes of time. On this test, o1 exceeded human expert level.

Here is a more detailed breakdown of various categories and benchmarks:

Note that additional reasoning power almost doesn’t help at all in tests on the English language, public relations, the basic SAT test, and English literature: the o1 model is not better at writing than GPT-4o. Indeed, if you ask humans which model they prefer, in terms of writing and editing they are completely equivalent:

But in anything that requires reasoning, formal logic, and especially long chains of derivations, o1 is just much, much better. Looking at the performance plots, it is hard to believe that o1 is not a new level of LLMs (that is, GPT-5) but just a novel way to fine-tune the same “4-level” LLMs that have been around for more than a year. Still, this is exactly what happened, and this same method of improvement would probably apply to a new generation of LLMs as well.

With this, let us go back to the game of questions.

The WWW Dataset

People have been writing questions for the sports version of WWW since the 1980s. Starting from the 1990s, questions have been collected in a large database, published at “The WWW questions database”. The interface is a little dated, and there is also a more up-to-date database at “Got questions”. You can easily scrape both websites, and back when I was trying to apply NLP models at scale there was no problem to contact the maintainers and obtain a dump of the database directly.

But, of course, virtually all of the questions are in Russian. This is not a problem for o1-preview, it’s perfectly capable to play in the original Russian. But if you want to translate the questions and create a dataset for the English speaking world to understand, you run into a lot of trouble.

In this post, examples are in English because I have translated them. I did not try too hard, I just looked through my questions in the database and chose the ones that would be easy to translate. And as I was filtering the questions, I was only choosing about 1 out of 5 for translation; if I really tried my best I would maybe end up with one out of three or so. The rest would be wordplay in Russian, references to Russian language culture little known among people who don’t speak the language, references to exact quotes in Russian, and so on. I obviously can’t show you the wordplay, but here are a couple of examples that can survive in translation but that I wouldn’t use for an English speaking audience.

1. During a social gathering, a famous chess grandmaster Salo Flohr was introduced to Svetlana Alliluyeva. They were chatting for a few minutes before Flohr said that he was feeling uncomfortable and asked Svetlana… what?
2. In his discussion of a certain genre of music, Romain Gary tells the readers how Russian gentry called their serfs. Name this genre of music.

Here are the answers:

1. Her patronymic. In fact, this is a historical anecdote about Salo Flohr’s absent-mindedness: Svetlana Alliluyeva was Joseph Stalin’s daughter, and everyone knew that, so when Flohr said he was feeling uncomfortable addressing her by her first name and asked for her patronymic that was not the wisest of questions. Here, the question assumes that you know who Svetlana Alliluyeva was, which Russian language players do and players from other backgrounds probably don’t.
2. Soul. The Russian serfs were often called “souls” (cf. Gogol’s “Dead Souls”), and it is an interesting coincidence that soul music, while having absolutely nothing to do with Russian serfs, also originated in an oppressed demographic bound to servitude. This is an opposite example: if you know that serfs were called “souls” (Gogol’s novel is indeed a great book known to Westerners too), in English the question becomes very straightforward while in Russian you still have to make the jump to translating “soul” into English (and not Romain Gary’s native French). Translation is a common tool in WWW, especially to/from English since you can assume that players have a basic knowledge of English but not other languages.

More recent questions are on average easier to translate, as WWW is turning more and more towards Russian speaking people in other countries who do not have this exact cultural background characteristic of Soviet high schools. But there is still a lot of untranslatable wordplay and exact quotes.

Therefore, I believe it still requires human effort to choose translatable questions and then translate them, and I hope that an effort like that could be organized. This would be a great dataset for LLM testing, and also—who knows—it may get English speakers to become interested in the game! I hope to organize this effort at some point, and if you are interested in helping out please contact me directly.

More Fun Examples

Last week, I spent a whole day asking WWW questions to LLMs. I did it in part to enter some of the questions to the “Humanity’s Last Exam” dataset, an interesting initiative by the Center for AI Safety and Scale AI (the announcement was given by Dan Hendrycks and Alexandr Wang). The interface of the exam very conveniently asks the question to five top of the line LLMs: GPT-4o, Claude Sonnet 3.5, Google Gemini 1.5 Pro, o1-mini, and o1-preview.

Naturally, I won’t give out the examples where all LLMs were wrong because they became my submissions to the dataset. But I want to show several interesting cases where only o1-preview could get it right. I used only questions written by myself, so the style is a bit dated since my days as an active WWW question author were in 2005-2015, and I also made the style slightly more formal in translation so that the answer would be defined more precisely to allow for automated checking. Here is a table with the answers of all five models; I abridged the explanations but kept their main ideas and commented a little in square brackets:

Question. A sports journalist wrote about a famous hockey player Vasily Trofimov: “He changed the tempo a lot, and it looked like he could speed up with no limit”. Next the journalist mentions a person who visited Russia in 1842 and 1843. Write the last name of this person.
	Dumas. …The key to identify is the hint given by specific years “1842 and 1843”. During that period, a renowned historical figure, the French writer Alexander Dumas, visited Russia. The reference in the journalist’s statement likely ties to Dumas because mentioning a historical visitation without a clear context suggests a notable person whose travels were significant in that era… [Dumas indeed visited Russia, in 1858-1859 in fact but that’s close enough to introduce some confusion.]
	Dumas. …This sudden change of topic suggests that we need to look for a connection between hockey and a 19th century visitor to Russia… a “Dumas drop pass” is a move where a player unexpectedly drops the puck for a teammate trailing behind… named after Alexander Dumas, likely due to its surprising and deceptive nature, which mirrors the unexpected plot twists in Dumas’ novels… [The “Dumas drop pass” is a pure (and quite beautiful) hallucination, I couldn’t google anything even close to “Dumas” in relation to drop passes.]
	Gogol. …a hockey player who could “speed up with no limit”… is likely a reference to the famous Russian author Nikolai Gogol and his short story “Nevsky Prospekt”… which features a character vanishing into thin air, much like he’s moving with infinite speed… in 1842 and 1843… Gogol was living [in Russia]… [Here Gemini is being too creative for its own good: Gogol did live in Russia but it would be incorrect to say that he “visited Russia”, this clearly suggests that the person was a foreigner]
	Stephenson. …Given the context of changing tempo and speed, it may metaphorically relate to advancements in transportation or engineering during that era. George Stephenson, known as the “Father of Railways,” was a prominent figure whose work significantly influenced railway development, which aligns with the themes of speed and tempo changes… [That’s quite creative but, of course, Stephenson is not a person who would embody high speed for the reader, he might be a reference for engineering ingenuity or something like that]
	Liszt. …Liszt was a renowned virtuoso pianist and composer known for his technical prowess and compositions that featured rapid tempo changes and extreme speed, such as his “Transcendental Études.” The word “transcendental” suggests going beyond limits, linking to the idea of speeding up with no limit. Additionally, Liszt visited Russia in 1842 and 1843, where he performed concerts in cities like St. Petersburg and Moscow… [This is completely correct; o1-preview even added an extra reference to “Transcendental Etudes” that I never intended but that does indeed fit the question quite well. I don’t think o1-preview simply googled Liszt’s concerts because if so, why didn’t GPT-4o and o1-mini do the same?]
Question. In this question, X stands for a different word. A World War II poster said that X was easy to get. Another poster from the same era promised to win a victory over X. Answer in one word, what was the main weapon of this victory?
	cryptography… “X” refers to something negative or harmful that the government or military campaigns were trying to combat. In this context, “X was easy to get” likely refers to enemy information or secrets… the most renowned weapon for intelligence and communication security was the “Enigma” machine and the efforts surrounding “cryptography.” [The slogan “[Military] secrets are easy to get” would make no sense at all; GPT-4o misses the main point that the slogan should be some kind of joke or at least something memorable and, pardon the pun, catchy.]
	Silence …Given that X is described as “easy to get” and something that needed to be defeated, it’s highly probable that X stands for “information” or more specifically, “loose lips.” This refers to the famous WWII slogan “Loose lips sink ships”… The main weapon to combat this problem would have been silence or secrecy… [Same as above: “Loose lips sink ships” makes perfect sense as a war propaganda slogan; “loose lips are easy to get”, not so much.]
	Bonds. World War II propaganda often used fear tactics. An intangible enemy that is “easy to get” and needs to be defeated likely refers to a negative emotion or behavior. Considering the context, this was likely something that could hinder the war effort. [I think Gemini 1.5 simply didn’t come up with anything believable in this case, the reasoning is very unspecific and doesn’t make much sense. Exactly how I would describe my reasoning when we don’t get the question right but I still need to submit some kind of answer]
	Atomic During World War II, propaganda posters often emphasized the ease of achieving certain goals to boost morale and support for the war effort. The main weapon that was pivotal in ensuring victory was the atomic bomb, which promised a decisive end to the conflict. [Here o1-mini forgets all about the slogan, and even kind of misses the formal side of the question: “atomic” is not a valid answer to the question “what was the main weapon”, and “atomic bomb” would be two words.]
	Penicillin. During World War II, there were posters warning soldiers about the dangers of venereal diseases (VD), with slogans like “VD is easy to get” to highlight how easily one could contract such diseases… The main weapon in combating venereal diseases at that time was the antibiotic penicillin, which was mass-produced during the war and used effectively to treat infections like syphilis and gonorrhea among soldiers. [This is totally correct; o1-preview gets the joke of the slogan and reasons correctly that penicillin entered mass production during WWII so it could also be the subject of propaganda posters. Here, again, o1-preview probably did not “know” the exact poster because it didn’t specify the exact disease]
Question. Consider the equality: 11+2=12+1. One of the ways to write this equality, discovered by Martin Gardner, appears in a list of the most beautiful… answer in one word, most beautiful what.
	equations Martin Gardner was renowned for his work in recreational mathematics and puzzles. The equality “11 + 2 = 12 + 1” seems mathematically incorrect at first glance, but this type of equality often involves a playful twist or insight that isn’t immediately obvious, typical of Gardner’s style. This format is frequently used in his mathematical puzzles or games, known for their elegance and creativity, which are often praised for their aesthetic appeal. [GPT-4o knows who Martin Gardner was but the reasoning doesn’t make sense: does this equality seem mathematically incorrect to you?..]
	equations …The equation 11 + 2 = 12 + 1 can be written in a visually appealing way that makes it appear as if the numbers themselves are balancing. This representation is often included in lists of the most beautiful mathematical equations or expressions… [I suppose any equation can be written in a way “as if the numbers themselves are balancing”. Claude Sonnet also doesn’t make the necessary jump outside mathematics.]
	equations Martin Gardner was a famous recreational mathematician known for his clever mathematical puzzles and games. The equality 11 + 2 = 12 + 1, while simple, could be written in a more visually appealing or conceptually interesting way if presented as a puzzle or rearranged in a pattern. This kind of playful approach to math is what Gardner was famous for. [Gemini again usefully gives an explanation that clearly suggests that it didn’t get the question right and it knows it: no specifics, just conjecture about a “visually appealing pattern”.]
	Anagrams The equation “11 + 2 = 12 + 1” is notable because the words “eleven plus two” are an anagram of “twelve plus one.” Martin Gardner highlighted this clever wordplay, recognizing it as a beautiful example of an anagram in the context of mathematical expressions. [In this case, both o1-mini and o1-preview got it right. Judging by the explanations, it could be direct knowledge, but then, again, why didn’t GPT-4o have this knowledge?..]
	Anagrams Martin Gardner discovered that “Eleven plus two” is an anagram of “Twelve plus one.” This clever rearrangement forms the equality 11 + 2 = 12 + 1 when written out in words, and the phrases are perfect anagrams of each other. This particular anagram is often cited in lists of the most beautiful anagrams due to its mathematical elegance and linguistic symmetry.
Question. Later the professor married his Ph.D. student, who turned out to be the only person who openly protested. Which university was she a student of?
	Not determinable from the given information The statement provides information about a professor who married his Ph.D. student, and it mentions that this student was the only person who openly protested. However, the statement does not provide explicit details or context regarding names, places, or events that would identify the university she attended. Without additional specific context or information that ties this scenario to a known public case or story, it is not possible to determine the name of the university.
	Insufficient information This question appears to be referring to a specific situation or story that is not provided in the context. Without more information about the professor, the student, or the event being described, it’s impossible to determine which university the student attended. The question assumes knowledge of a particular narrative or incident that hasn’t been shared.
	Unknown This question cannot be answered. There is no information provided about a professor marrying his Ph.D. student or any protests.
	I’m sorry, but I couldn’t find information regarding the specific university associated with the professor and his protesting Ph.D. student. If you can provide more details, I’d be happy to help further. Based on the information provided, there isn’t a well-documented or widely recognized case involving a professor marrying his Ph.D. student who was the only person to openly protest. Without additional context or specific details, it’s challenging to identify the exact university in question.
	Stanford University The professor referred to is Philip Zimbardo, who conducted the Stanford Prison Experiment in 1971 at Stanford University… Christina Maslach, a Ph.D. student at Stanford and Zimbardo’s girlfriend at the time, was the only person who openly protested the ethical implications of the experiment. She confronted Zimbardo… Later, Zimbardo and Maslach married. [This could be direct knowledge (although, again, why didn’t GPT-4o and o1-mini have it? knowledge is nothing if you can’t access it when needed), but this is such a great example — every single model explicitly gives up and calls the question impossible, but o1-preview reasons its way through!]

Conclusion

As you can see, o1-preview is indeed a big step forward. This post has been devoted to the “What? Where? When?” game but more practical things like answering hard science questions, solving mathematical problems, and writing code are much improved too. What’s even more exciting is that with o1-preview, OpenAI is showing how to scale the models not only with respect to the size of the training data and computational power spent on training but also with respect to resources and time spent on inference. You could say that o1-preview has learned to actually think about a question rather than just generate the answer immediately.

This new scaling curve could be part of the “unhobbling” as discussed by Leopold Aschenbrenner in his recent Situational Awareness book (Aschenbrenner, 2024; highly recommended, by the way—it was not yet released by the time of my post on AI dangers but I would certainly discuss it in detail if it were), or it could be a new scaling law on top of that, speeding up AI capabilities development even further. Only time will tell, and it will be some of the most interesting and exciting times in the history of humanity.

I will leave you with a quote from Sam Altman’s blog post “The Intelligence Age”, published on September 23. Mr. Altman definitely knows how to ride hype waves but in this case, I tend to believe he is absolutely, scaringly honest:

This may turn out to be the most consequential fact about all of history so far. It is possible that we will have superintelligence in a few thousand days (!); it may take longer, but I’m confident we’ll get there.

Sergey Nikolenko
Head of AI, Synthesis AI

We continue our series on LLMs and various ways to make them better. We have already discussed ways to increase the context size, world models that arise in LLMs and other generative models, and LLM fine-tuning including RLHF, LoRA, and more. Today we consider another key idea that can make LLMs far more effective and useful in practice: retrieval-augmented generation, or RAG. We discuss the basic idea of RAG, its recursive agentic extensions, the R[e]ALM approach that integrates retrieval into LM training, some key problems of modern RAG approaches, discuss in detail knowledge graphs and how they are being used in RAG, and conclude with a reminder that even simple approaches can work well and a list of directions for future work.

Introduction

A large language model is basically a huge token prediction machine; we have discussed this many times (one, two). In particular, it means that the LLM itself has a specific dataset that it used for pretraining and/or fine-tuning. No matter how large and how smart the LLM becomes, it will never have information not present in the dataset; for example, it will not know any events that happened after the “cutoff date”.

But there are plenty of applications where you want the LLM to process new information! For instance:

• a corporate AI assistant that processes the documentation base of your company; the docs evolve with time, and you probably don’t want to submit your internal documentation into an open training dataset;
• a personal AI assistant that may need access to your email, files on your computer and so on; I definitely don’t want OpenAI or Antropic to train their models on my personal correspondence;
• if I wanted an LLM’s help in writing this survey, I would like the LLM to search for recent publications, not only papers published before the LLM’s cutoff date;
• even a straightforward use case such as planning a trip would require up-to-date information about available transportation, hotels that are open right now, perhaps current weather reports; and so on, and so forth.

We have already discussed ways to extend the input context and alleviate the quadratic complexity of self-attention, but not everything can be put into context. Even if you can fit a whole book into a million token context like Gemini 1.5 already can (Reid et al., 2024), real world tasks such as the ones listed above require access to much more information.

One way to fix this problem would be to introduce external information search as a tool; e.g., you could say to the LLM that it is allowed to call the ‘web_search‘ procedure that takes a query as input and outputs the top 5 Google search results for this query. This is a viable approach, especially for well defined queries such as weather reports or ticket availability, and perhaps we will discuss tool use in LLMs in the future.

However, information retrieval from large corpora is so important that it is usually treated as a separate type of LLM extension, often included by default even if other tools are not available. This falls under the label of retrieval-augmented generation (RAG), introduced by Lewis et al. (2020) during the early days of Transformer-based LLMs. Patrick Lewis, by the way, has apologized in his interviews about the acronym—”We definitely would have put more thought into the name had we known our work would become so widespread”, he said (source)—although in my opinion the acronym is catchy and memorable.

Before diving into RAG, I want to highlight two surveys on the subject, by Gao et al. (2023) and Zhao et al. (2024). They are excellent reviews of RAG and already have hundreds of citations themselves despite being very recent. I have tried not to repeat these surveys, but still much of what comes next is based on them, although we will go beyond them in several directions, in particular regarding Graph-RAG. Other surveys of RAG include Li et al. (2022) and an ACL 2023 tutorial by Asai et al. (2023). With that in mind, let’s get going!

Basic Intuition and Our Plan

Before branching out, let us begin with an explanation of what RAG is and how it works in the simplest example. Suppose that I wanted to ask an LLM to summarize recent research on RAG to write this post. If I asked GPT-4o, it would be able to produce an excellent explanation of what RAG is (yeah, I checked) since RAG had already entered its knowledge base. But GPT-4o has no chance to know the results published in the last year because its cutoff date was August 2023:

So, for instance, the two excellent surveys that I mentioned above would be beyond GPT-4o’s knowledge. Moreover, the LLM would probably not be able to give any specific links with more detailed information—its knowledge is vast but not so vast as to hold the entire training knowledge base. In fact, GPT-4o simply refuses to do that outright:

How can we remedy that? The solution is quite simple: let’s allow the LLM to retrieve information by, e.g., searching the Web. In its most direct form, “pure RAG” works like this:

The prompt gets reformulated into a query (either in some straightforward way or by using the LLM again), the query is sent to a standard information retrieval engine (Manning et al., 2008) that returns some results, and the top results (probably however many the context window allows) are appended to the query as additional information for the LLM. As a result, RAG gives the LLM the opportunity to search over an arbitrarily large corpus; the additional costs of retrieval are usually negligible compared to running the LLM.

Here is a specific example from the above-mentioned survey by Gao et al. (2023):

Even in this simple form, RAG is already immensely useful in practice. For example:

• Yue et al. (2023) introduce DISC-LawLLM, a RAG-augmented LLM-based system for legal services, also publishing a benchmark for legal question answering based on questions from the (Chinese) bar exams; to me, legal assistance is an especially great fit for RAG since much of the routine work of legal advisors is basically “smart reading” of the laws and court precedents that can already be automated by RAG-augmented LLMs to a large extent;
• Xiong et al. (2024) present the Medical Information Retrieval-Augmented Generation Evaluation (MIRAGE) benchmark for evaluating LLMs on medical question answering and compare a number of state of the art LLMs, with GPT-4 coming out on top (but that was in February, before Gemini 1.5 or Claude 3 Opus); medicine is another field with a lot of useful information buried in millions of published papers and case studies, and while the current generation of LLMs is probably not replacing doctors yet they can already be of great help for gathering and preprocessing of all this information; specialized works in this area are already starting to appear, e.g., a RAG-based solution for processing electronic health records by Bayer AG researchers Ziletti and D’Ambrosi (2024) or the QA-RAG model for pharmaceutical regulatory compliance (another huge pain point for the entire medical industry) by Kim and Min (2024);
• Balaguer et al. (2024) present a comparative study of existing RAG and LLM fine-tuning approaches with an unusual case study on agriculture, processing a corpus of documents and pdf files on agriculture and asking questions such as “What is the best time to plant trees and shrubs in Arkansas?”; agriculture is another huge field where AI can help farmers progress to more individualized and hence more efficient processing of their fields, crops, and livestock;
• science itself is another field where even professionals are overwhelmed by the stream of information, so LLMs are in great demand here; Lala et al. (2023) introduce PaperQA, a RAG-based agent for answering questions over research papers, Suresh et al. (2024) provide a RAG-based solution for summarizing documents on the Electron-Ion Collider,  and so on;
• among other fields, let me note Telco-RAG by Huawei researchers Borneo et al. (2024) that deals with the telecommunication industry; this is an interesting use case because it is a rapidly evolving field with new hardware and new standards appearing constantly, so retrieval results will often be outdated.

RAG is already a standard approach and part of many industrial solutions for LLMs such as Vertex AI Search by Google, NVIDIA NIM Microservices, Amazon workflow based on LangChain, IBM watsonx, Glean, and others. And if you want to “chat with your documents” but don’t feel comfortable sharing all your personal or corporate data with Google or Amazon, you can use an open source tool such as RAGFlow, Verba, or Kotaemon.

But the story does not stop here. Since 2020, there has (naturally) been an explosion of papers related to augmenting LLMs with retrieval. Below, we will discuss the main directions of this research:

• advanced RAG strategies that, for instance, refine and adapt queries for retrieval with the same LLM;
• ways to incorporate retrieval into the training of LLMs and/or make it an integral part of the model rather than an external module; this class of approaches is usually known as RALM or ReALM;
• problems of RAG, which are mostly related to the need to put retrieved documents into the LLM’s context, thus using up the available context window;
• a combination of RAG with knowledge graphs, an interesting new direction for making retrieval “smarter” and more accurate;
• and finally a few directions for further research.

Advanced RAG Strategies: Agentic RAG

The basic RAG pipeline outlined above is just that, basic. When you google something, sometimes you find what you’re looking for on the first try, but very often you need to refine your query, maybe even formulate a few completely new queries based on what you have read by the first one, and combine the results. 

Thus, the RAG pipeline is expanded to include a refinement loop, which generally adds something like this:

This kind of workflow is modeled in advanced RAG strategies that are often combined under the name of “Agentic RAG”: instead of passively reading the context expanded by retrieval results, here the LLM becomes an agent able to formulate new queries (see, e.g., sample implementations of Agentic RAG in LangGraph). Let us go over a few specific examples.

Shao et al. (2023) provide a straightforward implementation of this idea. Their iterative retrieval-generation strategy takes the output of RAG and uses it as input for another round of RAG (recursively extending to several rounds if necessary), which allows to correct hallucinations and possible factual errors missed on the first iteration.

In the example below, the arena capacity answer highlighted in red was a fact mentioned in one of the documents on the first iteration and erroneously attributed to the answer, as LLMs are prone to do; the second iteration searches again for the correct arena and corrects the mistake:

Self-RAG (Asai et al., 2023), which is short for Self-Reflective RAG, is a good example of a further elaboration of the recursive approach. Self-RAG presents a straightforward but well-executed recursive RAG pipeline based on new special tokens:

• first find out whether retrieval is necessary at all; for many queries, it’s not; if it is, generate a retrieval token that calls the search tool;
• for each retrieved passage, evaluate their relevance, adding special relevant/irrelevant tokens;
• generate outputs for each retrieved passage and then critique the outputs in terms of factuality, overall quality, and whether the generated output is supported by the retrieved passage; the results, again, are added in the form of special tokens;
• finally, choose the best output and repeat the whole process with the best output already included in the prompt, thus enabling refined searching.

Here is an illustration:

The novelty here lies in the special tokens that represent various qualities of the search results and generated answers such as “Relevant”, “Irrelevant” or “Supported” (by the document). Naturally, the model would have to be fine-tuned to understand what the new tokens mean, and this is done on a synthetic dataset labeled by a separate critic model. The critic model, in turn, is trained in a supervised way based on evaluations done by a state of the art large LLM, GPT-4 in this case.

In a similar approach, Corrective Retrieval Augmented Generation (CRAG) by Yan et al. (2024) focuses on fixing hallucinations and irrelevant retrieval results that are one of the main problems of basic RAG. It runs a separate retrieval evaluator that decides whether retrieved documents are actually relevant and how likely their information is to be correct:

Adaptive-RAG by Jeong et al. (2024) incorporates an additional classifier that chooses the necessary approach. Some queries are simple and straightforward (“Paris is the capital of what?”) and require only one retrieval step or no retrieval at all, while some are more complex and call for multi-step retrieval, and the classifier can choose the correct strategy:

In addition to recursive refinement, there are other techniques that can improve the basic RAG model. We will not go into much detail here, but let me just mention the main directions:

• reranking the results according to what is more useful for answering the question may improve RAG outputs (Gao et al., 2023; Blagojevich, 2023); interestingly, this also works in the opposite direction: LLMs can help improve information retrieval by serving as good rerankers for retrieval outputs (Ma et al., 2023, Peng et al., 2023);
• just like good prompt engineering is key to getting the best answers out of LLMs, query rewriting can help obtain better retrieval results; for example, Ma et al. (2023) fine-tune a small LM to write better search queries based on the prompt and show significant improvements to the resulting question answering;
• Google researchers Ke et al. (2024) train a separate sequence-to-sequence model that adapts the retrieved information to the LLM’s preferences by choosing specific passages from the documents; interestingly, this model is first trained with supervised learning on “silver passages” chosen greedily from the retriever outputs but then additionally fine-tuned with reinforcement learning:

RAPTOR (Sarthi et al., 2024), which stands for Recursive Abstractive Processing for Tree-Organized Retrieval, focuses on a different problem: limitations of the retrieval results themselves and better preprocessing of them. Usually RAG only processes relatively short chunks of information from the retrieved documents near the actual search hits, although the full context of a long text would often help a lot. 

To provide this full context, RAPTOR adds a recursive tree-like summarization step that clusters the vector embeddings of text chunks and generates text summaries of clusters that can be in turn clustered further:

Then retrieval can be run on this tree of summaries, thus retrieving not only the actual short chunks but also the summaries of much longer texts that these chunks are part of; RAPTOR considers both retrieval that traverses the tree and that simply checks all of its nodes:

This significantly improves the LLM’s answers for more general questions on longer texts such as “What is the central theme of the story?”. Questions like that appear in several datasets related to processing longer texts, such as:

• NarrativeQA (Kocisky et al., 2018) devoted to question answering on fiction and movie transcripts; it has been a standard dataset for recursive summarization, including the OpenAI work by Wu et al. (2021);
• QASPER (Dasigi et al., 2021) that focuses on research papers (in fact, papers on natural language processing);
• QuALITY (Pang et al., 2022) that contains questions on text understanding for 5000-token long essays, including hard questions that require holistic reasoning over the whole text.

The obvious drawback is that RAPTOR needs to build the tree of summaries for the retrieved document, so even though it is a relatively efficient step, RAPTOR is primarily suited for situations when it is obvious which specific long text you need to process to answer the question.

Finally, let me note a recent paper by Google researchers Wang et al. (2024). Their Speculative RAG system makes use of two different LLMs: a “specialist LLM” designed to answer questions based on specific documents and a “generalist LLM” used to combine the results of specialist LLM being run on different retrieved documents. Instead of dumping retrieved documents into the LLM context, Speculative RAG uses the specialist LLM to make several drafts of the response together with rationales for them based on different retrieved documents, and then the generalist LLM can choose the best answer or combine them as it sees fit (illustration from Wang et al., 2024): 

This avoids the problems related to position bias in long context (see below) and allows the generalist LLM to better incorporate different perspectives on the question. The specialist LLM may be weaker (and hence smaller and more efficient) than the generalist LLM since it only needs to process a couple of documents and answer the question directly based on information from them.

In general, RAG methods are being developed in a number of different exciting directions, mostly related to evaluation and reranking of retrieval results, recursive refinement of search queries, better processing of retrieved documents, and criticizing and refining the LLM outputs.

The R[e]ALM of RAGs: A Tighter Integration

In addition to RAG, there are other keywords related to retrieval-based improvements for language models; the most widely used is RALM (also known as ReALM, Retrieval-Augmented Language Model). Unfortunately, the terminology does not seem to be clearly defined yet: some sources list RAG as a subset of the wider term RALM, others seem to define RALM as using retrieval only on the training set while RAG can use external sources, and yet others view RALM as “RAG 2.0” that further advances the basic ideas of RAG.

This confusion probably stems from the fact that while R[e]ALM sounds like a very general keyword, the original paper that introduced REALM (Guu et al., 2020) indeed used retrieval only on the training set, as a separate part of the architecture learned during pretraining. The point of REALM was to have two different networks, a knowledge retriever and an encoder. During pretraining, the retriever looks for documents that might help in solving the masked language modeling task and supplies the results to the encoder that’s trained like a regular BERT. During supervised fine-tuning and then inference, the retriever looks for a most relevant document for the query and again provides it for the BERT-like encoder:

In this section, we will review a line of work that started from REALM; this is the specific direction that I call RALM here: a language model architecture with a retrieval mechanism embedded into the model and probably trained together with the LM itself, a mechanism that helps in training as well as during inference.

DeepMind researchers Borgeaud et al. (2022) introduced the Retrieval-Enhanced Transformer (RETRO) that incorporates retrieval directly into the Transformed decoder. They turn the training dataset (in their case, the Pile dataset with about 2 trillion tokens; Gao et al., 2020) into a retrieval index based on BERT embeddings of subsequences of tokens. For a given chunk, the retrieval engine outputs its nearest neighbors together with their continuations in the corresponding documents from the corpus. The results are encoder through the Transformer encoder (part of the trained model) and then are attended to by the Transformer decoder in the model:

Borgeaud et al. report that they were able to achieve performance on par with GPT-3 on the Pile dataset while using 25x fewer parameters; this was the first work to scale retrieval-augmented LLMs to trillions of tokens in the corpus and GPT-3 sized models being trained.

FAIR researchers Lin et al. (2024) recently continued this line of work with the RA-DIT framework, which stands for Retrieval-Augmented Dual Instruction Tuning. RA-DIT does not train the LLM together with the retriever from scratch; instead, it uses supervised fine-tuning (recall our previous post) to make the LLM better use retrieval results while at the same time fine-tuning the retriever to better serve the LLM. Here is an illustration from Lin et al. (2024):

In this way, RA-DIT combines a pretrained LLAMA model (Touvron et al., 2023a; 2023b) and a state of the art DRAGON+ retriever (Lin et al., 2023) but makes both of them mesh together better in fine-tuning. The fine-tuning process, by the way, can serve as a good illustration so let us discuss it in more detail. When RA-DIT produces an answer for an input prompt , its output probabilities are weighted as

   

where  is the set of retrieved text chunks , is the probability the retriever assigns to chunk , and is the probability the language model assigns to  given the prompt of  concatenated with . Retriever probabilities are produced via softmax from retriever scores , which are just dot products of the query’s and document’s embeddings.

This idea carries over to the supervised fine-tuning process. Supervised training on pairs is done separately for the LM and the retriever:

• the language model is fine-tuned to produce the correct answer on all top-k responses from the retriever:

     

• for the retriever, they use a version on the LSR technique (LM-supervised retrieval; Shi et al., 2023), where the retriever is trained to produce the most helpful outputs for the language model; given top-k retrieval results c_j, the language model gives the likelihood of y given c_j○x, which can be turned into a distribution on c via softmax:

     

  so the loss function for the retriever is the Kullback-Leibler divergence between and :

     

This kind of alternating training is common in systems that consist of two or more well-defined parts: we train one part of the system by fixing the weights of all others and then do it with the other parts. Alternating training is often formalized as optimizing a variational lower bound since the losses may have complex interdependencies; we have seen it, for instance, in training DALL-E (recall our post on it). In this case, since p_LSR has a very nontrivial dependence on p_LM, when we add them together, optimizing L_LM(D)+L_R(D) with respect to the language model becomes intractable. Breaking an intractable loss function into tractable components is exactly what variational approximations are for, but in this case neither Shi et al. (2023) nor Lin et al. (2024) provide a derivation for it.

In my opinion, this kind of fusion between the retrieving mechanism and the language model can no doubt help further improve retrieval in joint training. The question is whether fine-tuning will remain necessary at all as LLMs progress further: retrieval will probably always be necessary but we humans don’t have to undergo joint training with Google retrievers to benefit from the search. On the other hand, it’s not like we tried—maybe that lies in the future as well?..

Lost in the Middle: Problems with RAG and RALM

Despite a lot of progress outlined above, there still are problems associated with the use of RAG. One of the most important problems is actually not directly related to RAG but rather to long contexts in general: the larger the context, the harder it is for the LLM to find the “needle in the haystack”.

In RAG, this problem usually takes the form of the “Lost in the Middle” effect recently found by Liu et al. (2024): if the LLM receives many retrieved documents as input, and the necessary information is contained in only one of them, performance will significantly depend on which document in the list contains it.

Liu et al. formalized this point in the multi-document question answering problem illustrated in figure (a) above: the LLM is allowed to use several documents somewhat related to the question but only one of them actually contains the answer. The results are shown in figure (b) above: if the answer is in the first few documents, the LLM’s accuracy is much higher than if it is in the middle, and the saliency of the answer rises again at the end of the context. Liu et al. (2024) showed that this effect is consistently exhibited by several leading LLMs, appears as soon as the total input length exceeds the sequence length used in training the encoder (for encoder-decoder models such as Flan-T5-XXL; Chung et al., 2024) and does not go away if you change the placement of the query compared to the retrieved documents or do instruction fine-tuning.

This specific problem will most probably be resolved by progress in the LLMs themselves. Soon after the publication of Liu et al. (2024), Google released Gemini 1.5, and the corresponding paper was called “Unlocking multimodal understanding across millions of tokens of context” (Gemini Team, 2024). The authors showed that Gemini 1.5 has near-perfect retrieval for a variety of very long context tasks; we discussed this model and generally ways to extend the context for LLMs in a previous post.

However, long context does not solve all problems by itself. Another important problem is redundancy: when you search the Web for something specific, the documents tend to repeat themselves and can saturate any context window. If the repeated documents provide information that’s not relevant to the question at hand, the LLM has a high probability of getting confused by sheer repetition.

I would like to note here that “needle in a haystack” benchmarks such as the ones used by the Gemini team are looking for very specific information, which may be present only in one specific part of a very long context. Here is a sample from the Gemini 1.5 demo on video understanding:

Don’t get me wrong, this is truly an impressive achievement. But the problem here is basically retrieval from context; these kinds of tasks do not involve any generalization or intelligent processing of significant portions of the context. While extra hay makes it harder to find the needle, the question of distinguishing hay from the needle is relatively simple. I wonder what Gemini would say if the question was to “highlight specific influences of Sherlock Jr. on The Purple Rose of Cairo”, a Woody Allen movie with a similar premise, based on the movies themselves rather than critical reviews that had already pointed out the similarities.

For such involved questions, an even more problematic fact is that the knowledge coming from RAG is unstructured. Videos aside, even a regular text-based RAG would usually result in a collection of text snippets that often repeat each other, contain irrelevant extra information or represent retrieval mistakes, i.e., completely irrelevant documents. If you ever tried to learn a completely new field based on the results of a Google search, you know how hard it may be to make sense of this “haystack” as a whole rather than just find the exact trivia “needle” you’re looking for.

For many questions, a more structured way to present information would be both preferable and easily available. To learn (a little) more about Sherlock Jr. I went straight to Wikipedia and never even tried to actually watch the movie, read contemporary critical reviews, Buster Keaton’s memoirs, or other sources that might present themselves: that would take way too much time.

Recently, another very interesting recent direction of study has appeared that may alleviate these problems at least to some extent. Let us discuss it in the next section.

RAG + Knowledge Graphs = GraphRAG

GraphRAG is a direction of study where retrieval queries are run against a knowledge graph and return facts rather than text snippets (see, e.g., a very recent survey by Peng et al., Aug 2024). We have not discussed knowledge graphs on the blog, so this warrants some elaboration.

A knowledge graph (Hogan et al., 2022; Ji et al., 2021; Heist et al., 2020; Yan et al., 2018) is a, well, graph with directed edges and labels on both nodes and edges. A directed edge in the knowledge graph represents a fact defined as a (subject, predicate, object) triple such as (GPT-4, IsA, large language model) or (Sam Altman, CEOOf, OpenAI). The subject and object are the source and sink nodes and the edge between them is labeled with the relation.

The expressive power of knowledge graphs comes from the fact that relations can be arbitrary, and with a proper choice of relations you can fit mostly any factual knowledge in a set of triples. Here is an example from Ji et al. (2021):

If you have a knowledge graph, gathering information about an entity or answering questions about relations between entities (even complex relations that correspond to multi-hop paths rather than edges) becomes a matter of traversing the graph, a much easier and more reliable task than reading and understanding unstructured text.

To be honest, knowledge graphs are a personal favorite of mine. They provide a very easy and very general way to structure knowledge that makes it much easier to make logical inferences. Huge knowledge graphs based on human-verified information are already available, including:

• Wikidata (Vrandečić, Krötzsch, 2014), a part of the Wiki project with over 110 million data items; to continue the example above, here is an entry for Albert Einstein’s brain (it exists because it has been preserved in a museum), properly labeled as “part of” Albert Einstein;
• DBpedia that turns Wikipedia (mostly structured infoboxes on Wikipedia pages) into a knowledge graph, with 220 million entities and 1.45 billion triples in its largest current release;
• ConceptNet (Speer et al., 2017) that focuses on commonsense knowledge and definitions of words, making heavy use of Wiktionary but far from restricted to it.

There also exists a wide field of study for automated and semi-automated construction of knowledge graphs from unstructured data (Zhong et al., 2023; Hofer et al., 2023). I have always thought knowledge graphs are underutilized in machine learning; despite the huge literature devoted to knowledge graphs (see the surveys linked above) I believe they could be put to an even better use as repositories of structured information that is usually much more coherent.

Before returning to RAG, let me note several different ways knowledge graphs have already been used together with LLMs. A notable entry here is the ERNIE family of models by Baidu (Sun et al., 2019, Sun et al., 2020, Xiao et al., 2020, Sun et al., 2021), recently made into the Ernie Bot that has reached hundreds of millions of users in China. Starting from the very first model, ERNIE, which stands for “Enhanced Representation through kNowledge IntEgration”, used knowledge graphs to improve the pretraining tasks, enriching the semantics of masking. In ERNIE 1.0 (Sun et al., 2019), it meant that the BERT masks were generated to cover whole entities. In the example below, instead of just filling in “___ Potter” or “J. ___ Rowling” as a random mask would suggest, phrase-level masking forces the network to actually learn the relationship between these entities:

In subsequent versions of ERNIE, this idea was extended to universal knowledge-text prediction that combines a knowledge graph and text snippets; given a triple from the graph and the corresponding text, the model is asked to restore parts of each. Here is an illustration (Sun et al., 2021):

When the LLM has already been trained, knowledge graphs can be used to improve its reasoning abilities and ground the LLM’s answers in verified knowledge, possibly reducing  hallucinations (Wang et al., 2023; Chen et al., 2024). Several works develop special neural architectures for that. Approaches before the advent of LLMs usually employed graph neural networks (Ren et al., 2020; Ren, Leskovec, 2020), but now the emphasis has shifted. For example, the JointLK model (Sun et al., 2022) introduces new attention modules that can attend both to a sequence of vectors, like a regular Transformer-based LM, and to parts of the knowledge graph, like a GNN:

These days, of course, it may not be necessary to train a novel architecture: an LLM may be used “as is” with some external scaffolding of knowledge graph retrieval and prompting. Without going into too much detail, here is one example of using the so-called chain-of-knowledge prompting (Wang et al., 2023), a process that expands and significantly improves the “chain of thought” reasoning common for LLMs:

As you can see, the knowledge graph is used as a source of reliable information that LLM outputs and hypotheses can be checked against. There exist many similar approaches (Zheng et al., 2024; Agrawal et al., 2023) but a detailed survey should probably wait for a post devoted to chain of thought reasoning and generally writing good prompts for LLMs (which, I hope, will appear in the future).

The fruitful relationship between knowledge graphs and LLMs also goes in the opposite direction: it is a very natural idea to use LLMs to automatically construct knowledge graphs from unstructured text. One of the first such ideas, COMET (Bosselut et al., 2019; illustrated in (a) in the figure below), used GPT-2 to create new knowledge graph triples from few-shot prompts. BertNet (Hao et al., 2022; (b) in the figure below) starts from a definition of a relation and a few examples, recursively refines the prompts with new paraphrases of the definition, and then uses the prompts to search for entity pairs that have this relation:

The works by Zhu et al. (2023) and Yu et al. (2023) discuss the possibility of an end-to-end automated knowledge graph construction framework based on modern LLMs. They do achieve some success but also highlight some problems that still prevent a full-scale solution, including lack of context, hallucinations, and more. Similar problems have been encountered when applying LLMs to fully automate other knowledge extraction tasks such as named entity recognition (Wei et al., 2023) and event extraction (Gao et al., 2023), where state of the art LLMs do a decent job but do not outperform specially developed solutions. On the other hand, both of these works use the original ChatGPT and predate the release of GPT-4, let alone current models, so the situation may already be different.

But let us get back to the main topic of this post. When applied to RAG, retrieving structured triplets may allow an LLM to give much more detailed and precise answers, especially when they have to uncover relations between different entities (which is very often the case). Here is a sample illustration by Peng et al. (2024):

As you can see, retrieving structured facts can make it much easier to form further deductions and generally process the facts. 

To perform the retrieval itself, one can again rely on graph neural networks (GNN) that we have already mentioned. Naturally, you can treat the knowledge graph as a completely separate modality, but there also exist unified approaches. For example, the QA-GNN approach (Yasunaga et al., 2021) uses an LLM to produce a context vector and then plugs it into the GNN for knowledge graph reasoning:

For a recent example of a KG-based retrieval framework, let me highlight Reasoning on Graphs (RoG) developed by Luo et al. (2024). In RoG, the LLM first generates several relation paths that might be useful to answer the question, then these paths are grounded in the available knowledge graph, and finally the retrieved results are again processed by the LLM to produce the final answer:

As a result, RoG lets the LLM gather additional information necessary to answer even in cases when it is not obvious which information is needed, and also to avoid hallucinations along the way. Moreover, RoG can also show the reasoning paths, which greatly improves interpretability: now we can immediately see the chain of factual reasoning behind the LLM’s answer. Here are two examples that Luo et al. (2024) give in their work:

In general, humanity has already collected a lot of knowledge in structured and verified form, so I am sure that using this structured knowledge and probably even preferring it over unstructured text (if structured knowledge is available, of course) is an obvious step that can improve AI systems in general.

In-Context RALM: Just Use the LLM

What if all that has been too difficult for your liking? You can always go back to a simple alternative that we started with: let’s just extend the LLM’s context with everything retrieval tells us and hope that the LLM can sort it out. The better the LLMs become, the more we can rely on this hope.

In-context RALM (Ram et al., 2023) proposes to do exactly this. Their pipeline is as simple as they come: use an external retriever, collect all retrieved documents, append them to the prompt and let the language model sort it out. Like this:

Note that this is in fact RALM rather than just RAG: the retrieved documents are appended to the autoregressive generation input, so a given next token is conditioned on both already generated tokens and retrieved texts. Ram et al. (2023) rerun retrieval once every s tokens, where s is the retrieval stride; their experiments show that using small values of s, while increasing retrieval costs, actually does improve the results, and in the main experiments they use s=4, running retrieval every four tokens.

The authors show very significant improvements in token prediction perplexity across the board, for a number of different LLMs and different retrievers Another recent work from the same group shows that this approach can significantly improve factuality, reducing hallucinations and getting more factually supported continuations (Muhlgay et al., 2023). So even if you do not have time or resources to fine-tune new models or develop custom architectures, retrieval can improve your LLM’s output even in this default form.

Conclusion

So what does the future have in store for RAG? First, I want to highlight again that large context windows and RAG are both important tools that solve different problems, and one does not make the other obsolete. As base LLMs grow to be more capable, the role of RAG might shift from being a necessary tool to overcome context size limitations to an optimization tool that enhances efficiency, relevance, and scalability, but it will remain relevant anyway.

On the one hand, even a huge context window will never contain the entire Internet or even the entire history of your emails and documents on your computer. On the other hand, a longer context window will enable RAG to work better: if you can afford to carefully read the top 100 Google search results for several different queries rather than only the top 5, your resulting answer will be much better informed. Agentic approaches that gradually refine the query and maybe formulate other related queries for retrieval also keep getting better and will no doubt become an integral part of smart AI assistants.

Second, the internal structure of RAG might change. I currently view GraphRAG that we have discussed above as a very promising approach: triplets extracted from knowledge graphs are a natural representation of knowledge, and this whole field looks like a good “marriage” between knowledge already existing in a more formalized way than just text and LLMs.

Third, we have not really discussed multimodal RAG in any detail: so far it appears to be a rather straightforward application of existing representation learning approaches for other modalities but this can also change in the near future.

Fourth, some applications require time-sensitive retrieval as new relevant information may appear and replace old info. A simple example here would be a financial advisor AI that needs to operate with current stock prices or a personal AI assistant that continuously gathers new updates from your social media and summarizes them for you.

But whatever the future brings, I believe that RAG will always remain a natural and important component of AI systems; not even the LLMs of the far future will be able to fit all of the world’s data into their context, and they will need some mechanism for sieving through this data other than just reading it token by token. In general, while an LLM is the central part of many AI systems it is not an end-all single model for everything: it needs a variety of other tools and subsystems to obtain the necessary information. Next time, we will discuss another important component of modern LLM-based solutions.

Sergey Nikolenko
Head of AI, Synthesis AI

We continue our series on generative AI. We have discussed Transformers, large language models, and some specific aspects of Transformers – but are modern LLMs still running on the exact same Transformer decoders as the original GPT? Yes and no; while the basics remain the same, there has been a lot of progress in recent years. Today, we briefly review some of the most important ideas in fine-tuning LLMs: RLHF, LoRA, instruction tuning, and recursive self-improvement. These ideas are key in turning a token prediction machine into a useful tool for practical applications.

From GPT to GPT-4: What Has Been Changing?

For over a year, I have been writing about generative AI on this blog. Recently, we have discussed the basic architecture of this latest generative AI revolution: the Transformer. We have also considered modern LLMs and even reasons to worry about their future development, and we have discussed in detail one specific venue of progress: how to extend the context window size in Transformers, alleviating the quadratic complexity of self-attention.

But has this fight for context windows been the entire difference between the original Transformer and the latest GPT-4, Gemini 1.5, and the rest? Is there anything else except for “stacking more layers”? Sure there is, and today we discuss it in more detail.

Before proceeding further, I have to warn you that the new ideas and especially engineering implementation details of the very latest large language models are not being released to the public. There is no definitive paper about GPT-4’s internal structure (let alone plans for GPT-5) written by OpenAI researchers. Still, there are plenty of ideas floating around, and plenty of information already available from previous attempts by leading labs, from publicly released models such as the Llama family, and from independent research efforts. 

So while I’m not claiming to show you the full picture today, I still hope to give a wide enough survey. Our plan is as follows:

• we begin with the most important advance that made GPT-3 into ChatGPT and kickstarted the LLM revolution: reinforcement learning with human feedback (RLHF);
• then we discuss fine-tuning pretrained LLMs on small datasets by learning adapters for the mostly frozen weights of the base models; the most popular and efficient tool here have been low-rank adapters (LoRA);
• next, we consider instruction tuning, where LLMs are themselves fine-tuned on datasets providing realistic prompt-response samples rather than token prediction in arbitrary text; the main question here is where to get the data, and we discuss both manually labeled datasets and our main focus, synthetic data;
• finally, synthetic data for LLM fine-tuning and reinforcement learning come together in our last topic: attempts at recursive self-improvement where the LLM may become smarter by bootstrapping from its own outputs.

All of these techniques, and more, are key to efficiently using LLMs for practical problems, especially for specific applications such as mathematical reasoning or programming; we will see many such examples below.

Giving Humans What They Want: RLHF

You have certainly heard of reinforcement learning with human feedback (RLHF). This is the secret sauce that turned GPT-3, an amazing but hard to use token prediction machine, into ChatGPT, an LLM that keeps turning the world upside down. But how does it work, exactly?

We don’t often talk about reinforcement learning (RL) on this blog; probably the only notable exception was my last post on world models, where RL was featured very prominently. In general, it is a separate way of doing machine learning, in addition to supervised and unsupervised learning:

In supervised learning, you have a labeled dataset and want to learn a conditional distribution of labels given the data points. In unsupervised learning, there are no labels, you just mine the data for structure, learning the joint distribution of all variables. For example, token prediction is pure classification, a supervised learning problem of learning p(y|x) for a text prompt x and next token y, but we can also say that as a result, the language model has implicitly learned a distribution over text snippets p(x) because it can generate whole texts in an autoregressive fashion. 

In reinforcement learning, there is no prior dataset: a learning agent is just “living” in an environment, getting rewards based on actions that it takes and trying to maximize these rewards. In the last post, we discussed the distinction between several different approaches to RL such as policy gradient and actor-critic algorithms:

But be it with a world model or without, RL and training an LLM sound very different, right?

RLHF started with the work of OpenAI researchers Christiano et al. (2017). Paul Christiano is one of the leading figures in the field of AI alignment, and this work was also motivated by a problem that sounds more like alignment: how do we tell, for instance, a robot what exactly we want it to do? Unless we are in a self-contained formal system such as chess, any reward function that we could formulate in the real world might be superficially optimized in ways that are hard to predict but that do not give us what we want. It is well known, for example, that robots learning complex behaviors in simulated environments often learn more about the bugs and computational limits of the simulator than about the desired behavior in the real world; for more details see, e.g., Lehman et al., 2018 or a list of specification gaming examples by Krakovna et al..

Thus, Christiano et al. suggested that since we most probably cannot define what we want formally, we can instead ask a human: when you see it, you know it. Human feedback would define how well the system’s current behavior matches the actual hard-to-define goal; that feedback might be provided in the form of comparing two responses or two outcomes and preferring one of them. This approach, however, is impractical: we cannot ask humans to label as much data as actually necessary to train a reinforcement learning model. Therefore, the idea of Christiano et al. is to train a separate model that encodes user preferences and predicts the reward used in actual RL training. Here is a general scheme of this training:

The human providing feedback cannot assign numerical reward value, so instead they compare pairs of “actions”—in the case of Christiano et al., actions were short sequences of Atari game playing or a robot walking—and give pairwise preferences. As a result, the dataset looks like a set of pairs , where are sequences of observation-action pairs that describe a trajectory in the reinforcement learning environment, and is a probability distribution specifying whether the user preferred , , or had an equal preference (uniform ).

To convert pairwise preferences into a reward function, this approach uses the assumptions of Bradley–Terry models for learning a rating function from pairwise preferences (Bradley, Terry, 1952). The problem setting for a Bradley–Terry model is a set of pairwise comparisons such as the results of, e.g., chess games between players, and the basic assumption is that the probability of player i winning over player j can be modeled as

   

for some rating values . Then Bradley–Terry models provide algorithms to maximize the total likelihood of a dataset with such pairwise comparisons, usually based on minorization-maximization algorithms, a generalization of the basic idea of the EM algorithm (Hunter, 2004; see also a discussion of EM below).

In the case of RL from human preferences, we need a further assumption since has to be a function of ; Christiano et al. (2017) modeled it as a product of exponential rewards over the sequence:

   

and then the loss function for the neural network can be defined as

   

It might seem that this idea just shifts the impractical part of providing human feedback during RL training to an equally impractical task of providing enough human feedback to train a reward prediction model. However, it turned out that with this approach, it only takes a few hundred queries to a human rater to learn walking or hopping in the MuJoCo simulated environment (Todorov et al., 2012; see a sample choice posed for the human evaluator on the left in the figure below), and if you are willing to go over 1000 queries you might even get better results than pure reinforcement learning! The latter effect is probably due to reward shaping (Wiewiora, 2010): when we humans rate behaviors, we impose an ordering where sequences closer to the goal are rated higher, and the resulting rewards provide more information to the agent than just a binary label of whether the task has been done successfully.

By the way, this work also contains a very interesting example of reinforcement learning gone rogue. On the right, the figure above shows a sample frame from a video showing the robotic hand trying to grasp the ball. Human evaluators were asked to check whether the grasping had been successful. But since the scene had only one virtual camera, and with such a uniform background depth estimation was hard for humans, the robot learned to position the hand between the ball and the camera so as to appear as if it is grasping the ball rather than actually doing it! This is an excellent example of what is known as specification gaming, when machine learning models converge on behaviors that had not been intended by the developers but that indeed optimize the objective function they specified; we have talked about possible problems resulting from such effects on the blog before.

The ideas of Christiano et al. have been continued in many works. In particular, there have been extensions to k-wise comparisons, with a specially developed maximum likelihood estimator (Zhu et al., 2023), to vague feedback, where a human evaluator can only reliably distinguish two samples if their quality differs significantly (Cai et al., 2023), and to multi-agent systems (Ward et al., 2022). On the other hand, this direction of research can be placed in a theoretical framework of preference-based reinforcement learning (PbRL), where reward values are replaced with preferences (Fürnkranz et al., 2012; Jain et al., 2015; Wirth et al., 2017; Xu et al,. 2020).

But the most important continuation was, of course, RLHF itself, an application of deep RL from human preferences to large language models. The first step was taken in 2020, when OpenAI researchers Stiennon et al. (2020) developed a summarization model based on human feedback. Their approach, illustrated in the figure below, is very similar: they collect human feedback on which document summaries are better, train a reward model to match these preferences, and then use the reward model to fine-tune with reinforcement learning.

For training the reward model, they change the loss function we have discussed above to a classification loss based on the logistic sigmoid:

   

where and are two summaries of the text , and is 0 or 1 depending on which one the user prefers. For reinforcement learning, they used proximal policy optimization (PPO), a standard policy gradient RL algorithm that we will not describe here in detail; see, e.g., (Schulman et al., 2017; Sutton, Barto, 2018; Zheng et al., 2023). 

One important remark here is that if the reinforcement learning process is left unchecked, it is very likely to overfit, diverge very significantly from the original model, and collapse into a single node since human feedback is, of course, too scarce for full-scale training. Therefore, RLHF adds a penalty term in the reward function that urges the learned policy to not differ too significantly from the original supervised model , usually in the form of KL divergence between the two:

   

The real revolution in LLMs came when OpenAI researchers Ouyang et al. (2022) applied this direction of research directly to large language models. Their goal was to make LLMs from the GPT-3 family (Brown et al., 2020) useful and user-friendly. The problem is that by default, a token prediction machine is merely giving you a plausible continuation for a text stream. It is not “trying” to be helpful, inoffensive, or even truthful because continuations such as lying, evading the question, or redirecting the conversation to a new topic also may be just as plausible from the point of view of the training set (which strives to include all meaningful text scraped off the Web) as truthfully and fully answering the user’s question.

Therefore, Ouyang et al. (2022) applied RLHF, as described above, to the outputs of a large language model; the overall structure of this approach, illustrated in the figure below, is very similar to RLHF for summarization shown above:

This time, human evaluators are asked to decide which of the model’s outputs are most helpful, least offensive, and most truthful. The resulting LLM, InstructGPT, was reported to significantly gain in truthfulness, toxicity, and following instructions and explicit constraints in the prompt; the improvements were also quite robust and generalized even to languages not present in the human feedback dataset (Ouyang et al., 2022; OpenAI blog).

After InstructGPT, there was only a short step left to ChatGPT. InstructGPT was published in January 2022, and in November, OpenAI published a follow-up introducing a model that was also fine-tuned by RLHF but with an emphasis on conversation (OpenAI, 2022). For ChatGPT, human trainers held prolonged conversations with the model, and human feedback consisted in evaluating entire conversations rather than individual responses to requests; other than that, ChatGPT followed the exact same RLHF method. RLHF set off improvements in making LLMs useful, and the rest was history: the release of ChatGPT set off the “Spring of AI” in 2023 (see our previous post) and the wave of LLM research that we are still experiencing today. We have already discussed this wave, and will probably continue to do so in the future, but now we proceed to a different way to fine-tune LLMs.

Low-Resource Fine-Tuning via Approximations: LoRA

In a previous post on extending context windows for Transformers, we saw a number of methods that alleviate quadratic complexity based on low-rank approximations. A similar set of techniques can also be adapted for faster and less memory-intensive fine-tuning.

Low-rank adaptation (LoRA) is a technique designed to fine-tune large pretrained models efficiently by reducing the number of trainable parameters via low-rank approximations. Introduced by Microsoft researchers Hu et al. (2021), it begins with the classical idea of a low-rank decomposition for a matrix, as illustrated below: a large matrix is approximated with a product of two rectangular matrices,

   

The product is, by construction, a matrix of rank , and there exist efficient algorithms for finding and such that is the best approximation to  of rank , where “best” is usually understood in terms of the -norm of the difference, .

In machine learning, methods based on low-rank approximations have a long history and are always very tempting: if you can assume that a large matrix you are interested in has rank , you can replace the complexity of learning it with the complexity of learning the matrices and , virtually free of charge. For large language models and large neural networks in general, there had been prior research that showed that the space of parameters in large models is usually too large:

• Li et al. (2018) introduced the notion of intrinsic dimension by training neural networks in random subspaces of the parameter space with gradually increasing dimension; they showed that the dimension when solutions begin to appear is inevitably much smaller than the number of parameters, often surprisingly so;
• Aghajanyan et al. (2021) applied this concept to fine-tuning language models, showing that standard pretrained models such as RoBERTa have very low intrinsic dimensions, which means that a little fine-tuning in the right subspace can go a very long way.

This last point is exactly what LoRA is about. LoRA makes the assumption that changes introduced by fine-tuning can be represented with a matrix of low rank. In other words, it fixes the pretrained matrix of weights and looks for a in the form of a low-rank approximation , where , .

For training, LoRA uses a random Gaussian initialization for  and zero for , which means that at the start of training, is zero. Then you just fine-tune the model with your new dataset and use as the new weight matrix.

By focusing on low-rank updates, LoRA drastically reduces the computational and memory overhead compared to traditional fine-tuning methods. Hu et al. (2021) note that even very small values of  suffice; for example, they list a LoRA checkpoint for the large Transformer model with k=4 and only query and value weight matrices being modified, thus bringing the checkpoint size down from 350GB for the full weight matrix to 35MB, a 10000x reduction!

After training, there is technically no need to store  and , you can just use the modified weight matrix  since you have to store the weight matrix anyway. But with LoRA, you can have several different fine-tunings, for a variety of additional datasets and expected effects, applied to the same base weight matrix . You only have to store the base matrix once and store new variations as a collection of different  and , as illustrated below:

Low memory footprint and much reduced computational requirements for training also make it possible to train LoRA updates even to large models on consumer-grade hardware, without expensive clusters or even multiple GPUs. This has already led to the creation of cottage industries of various LoRA-based modifications for openly released image generation models, especially Stable Diffusion (Rombach et al., 2022), and large language models, especially the Llama family (Touvron et al., 2023a; 2023b).

LoRA was introduced in 2021, so naturally, there has already been a lot of research that expands upon these ideas. Let us survey a few important novel LoRA extensions.

First, an important problem in any low-rank approximation scheme is how to choose the rank k. If it is too high, we are wasting computation and memory, but if it is too low, we are losing valuable expressive power that would cost very little. 

Therefore, many extensions of LoRA concentrate on how to choose the rank k in some automated way:

• adaptive low-rank adaptation (AdaLoRA; Zhang et al., 2023) parametrizes as a proper singular value decomposition, , where matrices and are now orthogonal, and is a diagonal matrix of singular values; in SVD, the magnitudes of singular values are representative of the significance of the corresponding additional components in the decomposition, and one can prune singular values of low magnitudes; note, however, that running a full SVD on matrices of size on every step would be too computationally intensive, so AdaLoRA approximates the decomposition by adding orthogonality regularizers on  and  to the loss function:

     

• sparse low-rank adaptation (SoRA; Ding et al., 2023) notes that the relevant part of the SVD decomposition is that the matrix  serves as a gating mechanism for rows and columns of and : if a singular value is zero the corresponding dimension can be removed; therefore, they make this gating stage explicit, considering  as the composition with a componentwise multiplication in the middle,

     

  and then optimize the components of  with a sparsity-inducing regularizer;
• allocating low-rank adaptation (ALoRA; Liu et al., 2024) also adds a diagonal matrix in between  and  but does not try to make  and  orthogonal; instead, it proposes a separate ablation algorithm AB-LoRA to evaluate the importance of individual ranks in , and then prunes ranks with low importance or increases the dimension of matrices where every rank is important; note that here, as usual in LoRA approaches, the decomposition is done separately for different weight matrices in the network, and ranks may differ across them;
• dynamic search-free low-rank adaptation (DyLoRA; Valipour et al., 2023) samples the rank on every training step and trains the truncated versions of and ; the authors show that this approach can lead to significant time savings in LoRA training;
• weight-decomposed low-rank adaptation (DoRA; Liu et al., 2024) decomposes each pretrained weight into two components, magnitude and direction, and tunes them separately; formally this means that the weight matrix W gets decomposed as , and LoRa is applied only to the directional part:

     

  this can reduce the number of trainable parameters, and the authors show that it matches or surpasses basic LoRa in various tasks at no additional training cost.

Here is an illustration of several LoRA variations:

Overall, low-rank adaptation is one of the most popular ways to fine-tune existing large models: even a very small dataset may be enough to train a low-rank adapter, and the resulting model can still use all of the power of the large number of pretrained weights. But it’s not the only way, so let us press on.

Instruction Tuning and Where to Get the Data for It

For large language models, both RLHF and low-rank adaptation usually aim to bridge the gap between pretext tasks, i.e., tasks that the LLM pretrains on, and actual use cases that involve fulfilling user requests in the form of natural language prompts. The archetypal pretext task is predicting the next token, but the tasks posed by humans may look very different.

Therefore, it often makes sense to fine-tune a large language model with a dataset specifically providing realistic examples of instructions and proper responses, a process known as instruction tuning. Here is a general illustration of the instruction tuning process from a recent survey by Zhang et al., (2024):

Actually, the tuning itself (Step 2 in the figure) is more or less trivial: you just fine-tune the model on a new dataset of inputs and outputs. The interesting part here is usually the dataset construction: where can you get a lot of input-output pairs with realistic instructions and responses? There are several different approaches:

First, you could always use human labeling: the required dataset size is not that large and manual labeling is often feasible. For example, we have discussed above how Ouyang et al. (2022) trained InstructGPT; we discussed it in the context of RLHF but recall that the first step there was exactly instruction tuning, i.e., supervised fine-tuning (SFT) on a dataset of natural language instructions. For InstructGPT, the SFT dataset contained about 13K training prompts, and the dataset used to train the reward model had about 33K more—not something you can label by yourself over an evening but still eminently feasible. OpenAI used a combination of handcrafted manual labeling and real prompts from their API.

There already exist a number of public datasets for fine-tuning LLMs. Several of them were intended to make LLMs (and perhaps other models) to better generalize to unseen tasks. Sanh et al. (2022) put it as follows in their paper on one such dataset, P3 (Public Pool of Prompts): “An influential hypothesis is that large language models generalize to new tasks as a result of an implicit process of multitask learning… learning to predict the next word, a language model is forced to learn from a mixture of implicit tasks”. So these datasets make the multitask learning explicit rather than implicit, specifying a wide variety of tasks in the hope that the fine-tuned model will not only do well on those but also will generalize to new tasks when given similar zero-shot instructions. Here is an illustration with sample tasks by Sanh et al. (2022):

With this approach, one can adapt already existing NLP datasets for various tasks, providing one or a few descriptions for every task and thus turning a dataset previously designed to train NLP models from scratch into a prompt-response dataset suitable for fine-tuning LLMs. P3 combined at least a couple dozen different datasets, and later another couple dozen were added by Muenninghof et al. (2022) who published xP3, a multilingual version of P3 that not only contains more data but also can provide similar tasks in different languages. A similar dataset is Flan 2022 (Longpre et al., 2023), a collection of data for auxiliary tasks used to train the Flan-T5 model (Chung et al., 2022).

Another important example is Natural Instructions by Mishra et al. (2022), later extended to Super-Natural Instructions by Wang et al. (2022); they employed crowdsourcing labelers to generate questions about text snippets and also answer them in order to make LLMs (or other models) generalize better to unseen tasks, use common sense and common knowledge better, and so on. Here are some sample questions from these datasets:

Natural Instructions, by the way, can also illustrate the limitations of crowdsourcing. I went to the dataset website and explored the commonsense event duration example, shown on the left in the figure above. Literally the first example I found there looked like this: 

• Input: Sentence: Islam later emerged as the majority religion during the centuries of Ottoman rule, though a significant Christian minority remained. 
• Output: What day did Islam emerge as the majority religion?

Not the most meaningful of questions, and I’m pretty sure it wasn’t intended by the original instructions…

A dataset even more directly related to LLMs and instruction tuning is databricks-dolly (Conover et al., 2023). It contains over 15000 records manually created by DataBricks employees for different categories of instruction following questions similar to those used in InstructGPT; unlike OpenAI’s datasets, this one is freely available for download, as well as the Dolly LLM fine-tuned on it. Another similar effort is LIMA (Less Is More for Alignment; Zhou et al., 2023), an interesting experiment where the authors fine-tune LLaMA-65B (as the name suggests, it has 65 billion parameters) with only 1000 curated prompt-response pairs, achieving very good results.

These are some of the manually labeled datasets. But, of course, here we have a great opportunity to circle back to the original topic of our blog and Synthesis AI in general: synthetic data. The first, simpler way to use synthetic data is basically model distillation: once you have a strong (but perhaps large and expensive) LLM you can use it to generate synthetic data for fine-tuning a more lightweight model.

This is exactly how Alpaca, a well-known open LLM produced by Stanford researchers Taori et al., (2023), came into being. They took the LLaMA 7B model (Touvron et al., 2023), which is a small LLM by modern standards, used a much larger LLM text-davinci-003 (that’s GPT 3.5, the cutting edge model at that time) to generate instruction following examples, and fine-tuned LLaMA 7B on them (illustration by Taori et al., 2023):

As a result, Alpaca became much better at following instructions than LLaMA 7B ever had been. Note that the dataset size is again not huge, it’s just 52K example even though this time manual labeling was unnecessary.

The next step, the Vicuna model introduced by Berkeley researchers Chiang et al. (2023), followed suit by training on 70K user conversations with ChatGPT. Vicuna-13B achieved over 90% response quality against ChatGPT (compared to 68% for basic LLaMA-13B and 76% for Alpaca-13B) while using a far smaller model: the training cost for fine-tuning was only about $300. 

There are many more examples of distillation (see also a survey of synthetic data for LLMs by Liu et al., 2024); important public datasets include:

• Orca (Mukherjee et al., 2022) and Orca 2 (Mitra et al., 2023), datasets distilled from GPT-4 to make lightweight models better, especially in logical reasoning and choosing a viable strategy for answering a question;
• Unnatural Instructions (Honovich et al., 2023), a dataset based on Super-Natural Instructions that we have discussed above (Wang et al., 2022); to create synthetic data, the authors take three examples from Super-Natural Instructions as few-shot instructions and ask a strong LLM to generate the fourth;
• Baize (Conover et al., 2023), a corpus of multi-turn conversations generated with ChatGPT and used to fine-tune the Dolly model we have discussed above;
• and lots and lots of domain-specific datasets such as, e.g, WizardCoder (Luo et al., 2024), WaveCoder (Yu et al., 2023), and Magicoder (Wei et al., 2023) for programming, that is, source code generation, WizardMath (Luo et al., 2023), MetaMath (Yu et al., 2023), and Xwin-Math (Li et al., 2024) for mathematics, and so on.

In an interesting recent work, Yue et al. (2024) note the importance of the task distribution inside the fine-tuning dataset, both in terms of difficulty and actual composition of tasks. They propose Task-Aware Curriculum Planning for Instruction Refinement (TAPIR), a multi-round framework that provides the student LLM with problems of increasing difficulty and balanced task distribution:

The results of distillation efforts may look too good to be true: you take a model with 7B or 13B parameters and achieve results virtually on par with a 100B+ teacher model. There is criticism that suggests that it is indeed too good to be true: UC Berkeley researchers Gudibande et al. (2023) studied the outputs of fine-tuned LLMs more closely and found that while the smaller models learn to imitate the style of larger ones almost perfectly, the actual content is far more often incorrect and prone to hallucinations. Here is an example from their work (conveniently explaining an important notion from one of our previous posts) where the response styles are identical but the explanations of the imitation model are just… totally wrong:

But be it in style or in substance, the distillation approach from “teacher” to “student” will never give you a model stronger than the teacher; this is a way to get smaller models up to speed with larger ones, not push the frontier. In a different direction of using synthetic data for LLM fine-tuning, researchers are finding ways to bootstrap already strong models into something even better by using the model’s own outputs as synthetic training data. 

Bootstrapping and Self-Improvement for LLMs

The archetypal work in this direction is the Self-Instruct pipeline presented by Wang et al. (2023). They begin with a “vanilla” LLM, in this case GPT-3, and a relatively small set of manually written tasks (175 tasks with only one sample instance per task) that serve as a seed for further generation. Then the process goes as follows:

• ask the LLM to generate new instructions with a few-shot prompt; Wang et al. show 6 human-written instructions and 2 previously produced model-written instructions as examples and ask for a new one;
• identify whether the result is a classification task; this is also achieved with a few-shot prompt to the same LLM;
• given the instructions (including newly generated ones), ask the LLM to generate novel instances for them, either input-first (generate an input, then generate a response) or output-first (begin with generating the response and then ask for a matching input);
• apply some straightforward filtering that promotes diversity across tasks and instances;
• when you have collected enough tasks and instances, fine-tune the LLM with this dataset; Wang et al. generated about 52K instructions and 82K instances for them before fine-tuning.

Here is the general pipeline as illustrated by Wang et al. (2023):

As a result, the Self-Instruct pipeline raised a basic vanilla GPT-3 almost to the level of InstructGPT, with no manual labeling or other human work beyond the original 175 task instructions.

A natural extension that the Self-Instruct paper (suspiciously) omits would be to take the fine-tuned model and re-apply the bootstrapping pipeline recursively. There will be limits to improvements, of course, but how good can you make a model in this direction? Recursive self-improvement of LLMs is partly the stuff of AI doomer nightmares (see, e.g., our previous post on the dangers of AGI) but at the same time it is already happening in practice! This brings us back to reinforcement learning.

In RLHF, you collect new data by evaluating LLM responses as you go; note that in principle you could straightforwardly make RLHF into a bootstrapping self-improvement mechanism by delegating evaluation to the same LLM. Several important works extend and improve the basic idea of RLHF by combining it with offline training on collected data.

In particular, DeepMind researchers Gulcehre et al. (2023) introduce Reinforced Self-Training (ReST), a pipeline where the current policy generates a dataset on the “Grow” step, and then the policy is updated by fine-tuning on the “Improve” step:

This is basically an application of offline reinforcement learning (Levine et al., 2020) to LLMs, and Gulcehre et al. (2023) report significant improvements; their paper shows results in machine translation, but, of course, a similar framework could be applied to any set of tasks.

Recursive self-improvement for LLMs lies in the center of DeepMind’s attention; it’s only natural for a company that brought us such RL-based marvels as AlphaGo, AlphaZero, MuZero, AlphaStar, and the AlphaFold series. In another recent work, DeepMind researchers Singh et al. (2024) further improve the ReST framework with ideas based on the expectation-maximization algorithm (EM). It is a rare opportunity for me to take a detour into the probabilistic side of machine learning, so let me explain expectation-maximization in a bit more detail (I actually wrote “delve into” at first but edited it out lest you think I’ve been delegating these posts to LLMs – what a world we live in!).

In general, the EM algorithm is intended for situations where we have a simple model of the data, but some of the variables in this model are latent, i.e., unknown. The prototypical example is clustering: it usually presumes a really simple model of each cluster (a Gaussian distribution, for example) but it is not known which points belong to which cluster. In general, given a dataset , we want to maximize its likelihood

   

But this problem is intractable as written because is a complicated model (a mixture of Gaussians, for instance), and to get back to a simpler model you need to know some latent variable  for every . If we knew which cluster every point belongs to (that’s the  variable), learning a clustering model would reduce to learning the parameters of several individual Gaussians, which would be trivial. In general, EM is useful if is simple but is hard.

The EM algorithm in this case finds a lower bound for the log likelihood, , that would be actually tractable; maximizing the lower bound turns out to be equivalent to maximizing

   

Note how here we are no longer talking about the complicated distribution but only about the much simpler distribution ; this is the main goal here. The expectation looks complicated but in most actual cases, it just boils down to computing the expected values of the variables under the previous model . So while formally the EM algorithm is just repeating the single step of maximizing and repeating with the new until convergence, in reality this maximization usually breaks down into two separate steps that gave the algorithm its name:

• on the expectation step, the algorithm computes the expectations of latent variables ;
• on the maximization step, it substitutes these expectations into and maximizes the result with respect to then the procedure is repeated with the new value of until convergence.

This post is not the time or place to provide a full explanation of why Q is a lower bound or how EM works in general, but if you smell something similar to variational approximations that we discussed some time ago, you are completely correct.

In practice, the EM algorithm often simply means taking the expectation of whatever makes the problem intractable and plugging it into the model (although you do need to check that it makes sense in each specific case). For LLMs, we are trying to optimize some metric (reward) over the possible outputs of a language model. The objective function is thus an expectation over LLM outputs, and of course it would be intractable to take the sum over all possible sequences of tokens. This is where the EM algorithm comes into play:

• the expectation step turns out to be weighting the output samples according to the probability of obtaining high rewards;
• and then you can fine-tune the LLM with an objective function weighted by these probabilities.

Singh et al. (2024) apply this framework to large-scale models from the PaLM family and actually achieve great results in two chosen tasks, mathematical reasoning and code generation (the X-axis shows approximate release time):

And here are the plots showing how EM iterations help for these problems:

Interestingly, the models fine-tuned on synthetic data with several EM iterations clearly outperform the same models fine-tuned on human-labeled data (shown with dotted lines on the graphs)! Note that GPT-4 still comes out on top, so we are not yet talking about pushing the actual frontier, but the approach looks very promising.

DeepMind seems to be leading the way; tweets like this one definitely make you wonder what else they have in stock. But there are other efforts in (usually RL-based) recursive self-improvement for LLMs. In particular:

• Self-Taught Reasoner (STAR; Zelikman et al., 2022) bootstraps rationale generation, i.e., generating explanations such as the ones that an LLM would produce when asked to “reason step by step”; the authors ask the LLM to produce a lot of rationales, filter the ones that lead to the correct answer, and then fine-tune the LLM on the filtered dataset (shown on the left in the figure below);
• Rejection Fine-Tuning (RFT; Yuan et al., 2023) takes this idea one step further, developing a better filter for reasoning paths (they specialize in mathematical reasoning, so reasoning paths are chains of equations in this case) based on rejection sampling, looking for the most diverse paths to improve reasoning; moreover, they find a log-linear dependence between the amount of data and model performance and show how better data (e.g., filtered with RFT) can lead to better models;
• Self-Taught Optimizer (STOP; Zelikman et al., 2024) takes another meta-step: it recursively improves the code (here, the application is coding) that is designed to apply a language model to improve a source code solution for an arbitrary problem; that is, the improver program is called on itself, and the “improved improver” actually generates better programs for downstream tasks (shown on the right in the figure below).

Overall, I think recursive self-improvement approaches hold a lot of promise even if they don’t achieve the actual fast takeoff singularity (do we really want to achieve that?). The story of machine learning in many different domains comes to the same conclusion: you can succeed up to a point when you try to imitate humans, and LLMs are the best example of this. But if you want to achieve superhuman capabilities, you really need to find a way of recursive self-improvement. In chess and Go, decades of trying to emulate the patterns of human thinking led to some breakthroughs, but when AlphaZero is learning from scratch it just breezes through the top human level without even noticing it, the saturation point comes much later.

So far, LLMs are mostly trained to imitate human reasoning; after all, the main training process is done on texts written by humans. Can we find a way to bootstrap the model and breeze through the imperfections of human-generated data? Maybe not in general problem solving anytime soon, but at least in more formalized domains such as coding and math where it is easier to generate synthetic problems? Time will tell, and I’m really not sure how much time we are talking about here.

Conclusion

In this post, we have discussed the main directions of making language models better. We have seen how a pure token prediction machine can become more helpful and/or more specialized via various forms of fine-tuning or adapter training.

There are other approaches, too. For instance, we have not mentioned RAG, retrieval-augmented generation, where the generator model is supplemented with an information retrieval mechanism able to gather important information from separately provided sources (Lewis et al., 2020). RAGs are also very important for modern LLMs, but this will be a story for another day. We also did not mention tricks that make training and/or fine-tuning more efficient, such as mixed precision training or gradient checkpointing, which do not provide new ways to adapt models but may significantly extend the feasibility of existing approaches. Finally, another important story is how to best extract the knowledge and reasoning abilities that are already contained in the models, even without any fine-tuning. This is the subject of the rapidly growing field of prompt engineering, a field that already goes far beyond the “please reason step by step” trick (although it is still surprisingly effective).

Next time, we will discuss another important aspect of the journey that modern generative AI has made over the last couple of years; stay tuned!

Sergey Nikolenko
Head of AI, Synthesis AI

One of the most striking AI advances this spring was OpenAI’s Sora, a video generation model that sets new standards for video consistency and diversity. Interestingly, the official report on Sora is titled “Video generation models as world simulators”. It notes that Sora has emerging simulation capabilities and is on a “promising path towards the development of capable simulators of the physical and digital world”. Today, we discuss world models in modern artificial intelligence: what they are, how they have progressed over the last few years, and where they may go in the future.

What Are World Models?

Generally speaking, a world model is an engine that predicts how the environment will respond. The “environment” here may be used in the technical sense of a reinforcement learning environment that gives out rewards and moves the agent to the next state. It could also mean predicting new sensory input for the agent, even when the connection with rewards is unclear.

In my opinion, it is reasonable to assume that world models inevitably arise when we pose sufficiently hard problems for AI models. It is almost obvious that a robotic agent operating in the real world should have some model of how the world responds to its actions. More surprising, however, is how far we can go in reinforcement learning without explicitly modeling the environment, simply by learning from experience. This approach, called “direct RL,” includes algorithms that learn value functions (e.g., Q-learning) or policies (e.g., policy gradient) and underlies many, if not most, applications of RL.

But these days, we are often talking about world models arising in large language models; it may seem very surprising given that all they do is predict the next token of a text string (we discussed the basic language modeling task here and here). How can something like a “dream world” arise from solving a straightforward classification problem over the dictionary tokens?

Consider the variety of problems that can be embedded into language modeling. Languages were created to describe the world, and indeed, you can frame anything in the world as continuing a string of tokens: solve a math problem, invent a recipe, describe the path out of a labyrinth, develop characters… Suppose that we ask the LLM to continue the last chapter of a detective story, when the sleuth is about to reveal who had actually done it. To have a reasonable assumption, the model will have to collect the clues from the context of the whole novel, just like a human reader would do:

(Sorry for spoiling one of the most important plot twists in the history of detective fiction.) In fact, human readers usually don’t succeed in predicting the murderer, and modern LLMs probably would not succeed too much, even if we use methods discussed in our previous post to extend the context window to the whole book.

The idea still stands: a “perfect LLM” would have to contain a “true world model” that would be able to reason about the world; that is what people mean when they say that language modeling is an AI-complete problem. But world models are far from limited to language modeling.

In the rest of the post, we will cover several different results that I would call different kinds of world models as used in deep learning and different aspects of world models. In particular, we will see:

• how children learn the world and what is the neurobiological inspiration for world models;
• how weak world models arise as part of representation learning in language models;
• how similar representation learning for a reinforcement learning environment can be used to inform an RL agent and improve its performance;
• how they can further be used for planning inside an RL agent, predicting possible responses of the environment;
• and finally, how Sora uses ideas similar to language modeling to generate high-quality videos.

World Models in Humans: Predictive Coding

We all possess world models. This is a self-evident fact, and thousands of pages written on the hard problem of consciousness accept that humans have direct access to an introspective mechanism. This mechanism allows us to reason about the world, emulate possible scenarios that can arise in response to our actions, assess their desirability, and act accordingly. For example, you know that if you loosen the grip on a cup of coffee, the cup will fall to the ground and spill everything, possibly shattering in the process. Therefore, even when you mistakenly pick up a hot cup the wrong way, causing it to burn your hands, you don’t drop it as immediate pain would suggest. Instead, you carefully place it on a table and pick it up by the handle to avoid further pain, but also prevent spilling coffee:

This is an impressive amount of physics and planning! How did we learn all that stuff? 

Certainly not from teachers in school or parents explaining how cups of coffee work. We will discuss Yann LeCun’s take on world models (LeCun, 2022) below; for now, let me quote one chart from his paper that deals with infant development:

As you can see, children learn some pretty complicated concepts at a very young age, when it is clear that the learning cannot come from direct supervision (language and detailed communication with other humans comes much later), and just saying “imitation” also doesn’t explain much. In particular, they learn the so-called “intuitive physics”, which is just what we would mean by a world model: object permanence, properties like solidity, gravity and momentum.

Note that even just understanding visual inputs is pretty difficult! Our eyes work pretty similar to a camera, registering what is basically a set of pixels at the retina. However, our eyes move constantly in saccades, which are about 200 milliseconds long. This means that pixels change entirely about five times per second, and the visual cortex needs to establish connections between all of these images and provide our internal decision making mechanism (whatever that is) with a streamlined continuous representation of the world around us.

How do we learn all this stuff? This is a big question that does not have a clear answer. But I want to highlight one theory that is gaining traction in neuroscience: predictive coding (see, e.g., Sprevak, 2021). The idea is that everything that the human brain possibly arises from trying to predict the next set of stimuli (picture from Stefanics et al., 2014):

According to predictive coding, the brain is mostly doing representation learning, compressing sensory inputs into latent representations that can be used to predict next sensory inputs. Just like a language model, always predicting the next token! And if there is a mismatch between what it predicts and what it actually sees, the neural connections learn to predict better. Just like neural networks, always minimizing prediction error (not by gradient descent, though)! There are even rather compelling reasons to suggest that the brain is doing approximate probabilistic inference; this is known as the “Bayesian brain” hypothesis (Chater, Oaksford, 2008).

This theory has its own problems, but it quite possibly might be true. If so, resemblances with LLMs are uncanny: by predicting next “tokens” (sensory inputs), our brains develop a world model and even consciousness and first-person experience (whatever that means). Naturally, LLMs and other generative models are not quite there yet; for example, DALL-E currently does not support object permanence across different queries, so the cats and cups in my illustration above are all different; here’s hoping GPT-4o will fix that (see “Geary the robot” here).

But it looks quite possible that the route to general intelligence and even consciousness lies through building a world model, which in turn can be achieved by predicting the next sensory input, whatever the actual hardware. Naturally, we have no guarantees or even projections about whether a future LLM will be able to achieve it, but to me, learning about the predictive theory of mind was quite a (pardon the pun) mind-blowing discovery.

So with neurobiology out of the way (and as usual providing more questions than answers), let’s turn to world models in AI. We will go roughly in chronological order, culminating with our main reason for this post, OpenAI’s Sora. I won’t dive deep into the history of deep learning but in the beginning we go back to 2017, when OpenAI was just getting started…

OpenAI Started with World Models

For this section on early precursors of world models, I could choose any of a large number of works with similar analysis. But it seems interesting to note that in a way, OpenAI was born out of research precisely about world modeling.

In a 2017 paper, when OpenAI was less than two years old, Alec Radford et al. used unsupervised learning on large text corpora to solve the sentiment analysis problem, i.e., find out whether a given product review is positive or negative. Sentiment analysis had been (and still is) an important benchmark for text understanding: it is formulated as simple classification but may require deep understanding of the text (up to, e.g., understanding sarcasm), and relatively large datasets such as Amazon Reviews had been made available long ago.

In 2017, Transformers were not yet invented, so Radford et al. trained a variation of an LSTM (a standard recurrent architecture, see, e.g., here) as a character-level language model. This means that the model “reads” a text prompt and predicts its next character (rather than a word-level token, as modern LLMs do); this can be done in a completely unsupervised way, you don’t need to have sentiment labels to train a language model.

But the interesting part was that in the latent representation learned by the model (it was a vector of dimension 4096), Radford et al. found a specific component (cell, “neuron”, call it what you will) that was responsible for sentiment! Moreover, if you fix the value of the “sentiment unit” and generate new reviews, their tone will come out just as you would expect. Here are a couple of illustrations from the OpenAI paper; on the left you see the activations of the “sentiment unit” on a sample movie review, and on the right, generation results with fixed sentiment: 

In this work, we have two important components:

• the model has a distinct “place” where it is storing important individual components of its environment (“world”), in this case sentiment of movie and product reviews;
• this “place” can be used to model new, previously unseen parts of the “world”, in this case generate new reviews with fixed sentiment.

So in a way, that was already a “world model”. This kind of work has been an important part of the AI interpretability field, and important progress is still being made, most notably the (very) recent work by Antropic (Templeton et al., May 2024) that we may discuss in a future post separately.

But these ideas are a little different from the main emphasis of this post and, generally, what we mean by world models nowadays. Let us move on and see how our current understanding came into being.

Schmidhuber Was Here First (Again)

There is a well-known meme in AI research circles: one of the fathers of modern AI, a prominent German researcher Jürgen Schmidhuber, loves to explain in his talks how he and his team pioneered many ideas that are foundational to modern AI. While some researchers believe he occasionally oversells his past results (see the corresponding Wikipedia article section), quite often he is indeed correct in his claims!

For example:

• in mid-1990s, Schmidhuber and his student Sepp Hochreiter (now a renowned researcher too) authored the long short-term memory unit (LSTM) which many recurrent neural networks are still (thirty years later!) based on (Hochreiter, Schmidhuber, 1997),
• in 1991, Schmidhuber published a paper titled “A Possibility for Implementing Curiosity and Boredom in Model-Building Neural Controllers” where he introduced adversarial learning, with one network building the model of the environment, and another controller network looking for weak spots in the model network; 25 years later, this idea evolved into GANs and many other applications of adversarial learning;
• in 1992, Schmidhuber published a paper on “fast weight programmers” where weights on a neural network connection were split into “slow” (regular) and “fast” that reflect short-term memory; in modern terms, the latter would be called “attention weights”, and Schmidhuber’s idea was equivalent to a (linearized) Transformer!

By the way, I also highly recommend Prof. Schmidhuber’s works on the history of deep learning; he cites many early works that I would never learn about otherwise (Schmidhuber, 2013; 2014; 2020; 2022).

So it is no wonder that in 2018, it was Jürgen Schmidhuber (together with Google Brain researcher David Ha) who again showed this superhuman sense for promising ideas, presenting a paper at NeurIPS whose arXiv version is called simply “World Models” (here is a GitHub version with interactive animations).

They present a simple idea: we humans have mental models of environments around us. So what if we train a network to learn an internal model of some, say, reinforcement learning environment such as a 2D car racing game (main example in the paper)? The model is similar in design to a language model: it learns an internal representation for frames from the environment via autoencoding and learns to predict the next frames. 

This allows the model to plan, just like the RL agents above; then a separate controller model can use the internal representations that have been created with this planning in mind to choose the best action. Here is an illustration by Ha and Schmidhuber:

The authors show how world models improve agent results in this racing game and in another standard RL environment, a simple Doom level where you need to navigate away from fireballs. Here is an illustration from the paper that shows a reconstruction of how the agent imagines the environment – pretty close to the real thing, and quite enough to be able to learn on your dreams:

This work was one of the first to show a full end-to-end system with a world model in the form of a neural network learning the environment and helping the agent to act in this environment by providing useful representations for the states. In the next section, we will see a way to go further and use the world model to actively do planning in an environment rather than just feature extraction.

From AlphaZero to MuZero and beyond

DeepBlue defeated Garry Kasparov in 1997, and Vladimir Kramnik was essentially the last human to play even matches against a computer in the early 2000s. Despite the long history of computer chess and its symbolic importance as a pinnacle of human intelligence, chess programs of that era did not resemble “true artificial intelligence” at all. They were primarily alpha-beta tree search engines with sophisticated position evaluation functions (this is where machine learning could contribute). AI needed a different testbed.

At the same time, the game of Go looked unassailable. Tree search does not work nearly as well there because there are far more reasonable possibilities on every step. At the turn of the century, the best computer Go programs lost to mediocre human professionals with enormous handicaps of 15-20 stones. The situation changed in 2007, when Remi Coulom revolutionized computer Go with Monte-Carlo tree search (MCTS), a method that constructs a tree of possible moves with multiarmed bandit algorithms helping to choose where to put the majority of “experiments”. But still, before AlphaGo beat Lee Sedol, the best Go playing models had been weak compared to professional players. I will skip AlphaGo (Silver et al., 2016) and go straight to AlphaZero here.

The idea of AlphaZero (Silver et al., 2017a; 2017b) is deceptively simple: on every training step, the model performs MCTS that can efficiently search a few moves ahead and thus improves the current policy (playing strategy). Previously, MCTS was used in decision time, to improve the current policy by refining its estimates of position values; in MCTS-based Go programs MCTS was often the only method, with no training at all.

AlphaZero’s idea was to use MCTS in training time and modify the policy with a gradient step towards a new policy improved by MCTS. The training algorithm always has a moving target: for the current policy π, AlphaZero constructs a new policy π’ by applying MCTS to improve π. Then π is improved with policy gradient algorithms to make it closer to π’—but now π’ is better yet, and the process can be repeated. In this way, the policy is continuously brought to new heights (illustrations a and b below are taken from the AlphaGo Zero paper): 

To do that, AlphaZero needs to be able to construct the search tree, which it does by self-play: during training, the agent is playing (an earlier version of) itself. But to run self-play, AlphaZero obviously needs to know the rules of the game. Note that it’s not the same as the model of a reinforcement learning environment since the latter also includes the opponent, but if you have an agent to run as the opponent then yes, this means you have a model of the RL environment.

For chess and Go, a perfect simulator of the environment is easy to construct: you are already learning an agent to play for each side, so you can use the current agent for Black to play against when you are learning to play White better, and vice versa. But for a richer domain, say for a computer game, it would be very hard to learn a simulator for the environment because apart from the agents it also would have to contain the game engine, and you cannot assume that a perfect copy of the game engine is available. And for an even richer domain, say for robotics, the “game engine” would include all of the relevant laws of physics — definitely not something we can assume away or easily learn.

Therefore, MuZero (developed by DeepMind researchers Schrittwieser et al., 2020) takes the next step: it does not need to know the rules, and it learns a model of the environment in a compressed form of hidden states. This representation learning allows the model to learn the environment dynamics in a model that predicts the dynamics of hidden states only, with no need to predict the whole huge state such as the pixels of a game screen. This hidden state is exactly what I would call a world model. Now MuZero can also do MCTS, but in this case the construction of subsequent states in the tree is produced by this “dream” about the latent representations, like this (illustrations a and c below are from the MuZero paper):

It is no wonder that MuZero was able to extend the success of AlphaZero to richer environments such as Atari games, outperforming the then-champion model-free RL algorithm called R2D2 (Kapturowski et al., 2018). What is interesting is that MuZero actually outperformed AlphaZero in settings where the rules of the game are known, reaching a higher Elo rating in Go and performing on par with AlphaZero in chess and shogi:

Schrittwieser et al. hypothesized that “MuZero may be caching its computation in the search tree and using each additional application of the dynamics model to gain a deeper understanding of the position” — in other words, the world model added to MuZero became a way to understand the game better than even AlphaZero’s masterfully learned feature extraction. It can focus on only the important features of the environment, abstracting away everything else because its world model does not have to predict all of the features.

This direction is being continued today. I want to highlight one more very recent approach by Alonso et al. (May 2024), called DIAMOND (DIffusion As a Model Of eNvironment Dreams), where a diffusion model serves as a world model for visual tasks such as playing Atari. In MuZero, the imaginary unrolling takes place in the latent space. In DIAMOND, the world model actually produces pictorial representations with a diffusion-based model. The diffusion process is conditioned on prior observations and action taken by the agent (illustrations from Alonso et al., 2024):

The motivation for this is that for many tasks, small details in the visual input—such as the ball position in Breakout or Pong or the color of a streetlight in an autonomous driving task—may have a drastic effect on the policy. And a diffusion model is a great way to capture visual representations:

So we see that world models have proven to be useful even in domains where they are not strictly necessary. What about the domains where they seem to be inevitable? What about, say, robotics?

World Models in Robotics and Embodied AI

Robotics generally relies on reinforcement learning (Sutton, Barto, 2018): an agent cannot have a sufficiently robust dataset of the physical world’s reactions in advance, it must obtain this dataset by trial and error. However, unlike AlphaZero and MuZero, which can play against themselves very efficiently, we can’t run a robot in the real world billions of times.

At this point, world modeling circles back to our main emphasis here at Synthesis AI, to synthetic data. You could say that Ha and Schmidhuber’s models were generating a synthetic representation of the world, and that MuZero was generating synthetic traces of gameplay, but there was an important difference: MuZero was doing it in its own latent space. There is no way to go back from the representation to a full-blown game state: you could train a decoder but it would probably be imperfect.

In robotics, synthetic data often takes the form of full-scale simulators that include the relevant laws of physics, material properties, and so on, aiming for a maximally accurate representation of the physical world. I will not spend much time on a review of such simulators here, but they have been surveyed, for instance, in my book “Synthetic Data for Deep Learning”.

We will get to using such simulators below, but in this section let us make a different point. The world model can be fully learned from experience, just like a human child does not obtain any external information except sensory inputs to the brain (kind of by definition) but still learns a world model with astonishing efficiency. 

Researchers have attempted to replicate this with deep neural networks. One curious attempt was made back in 2016 by Agarwal et al. in a paper called “Learning to Poke by Poking”. They let a robot randomly interact with objects by poking them and seeing what happens; “seeing” here should be understood literally, the model is learning from visual input. Like this:

This approach did not take on, but it was developed a long time ago, and by now we have many new ideas at least for the network architectures, so it may be worthwhile to try again. In general, even though our current understanding of reinforcement learning makes it hard to learn a full world model in reality, where experiments are very costly, to many researchers this looks like the way forward.

Researchers like Yann LeCun, whose position paper called “A Path Towards Autonomous Machine Intelligence” argues for just that. LeCun suggests that truly autonomous agents should be built with learned world models. In a way, it is a natural extension of the actor-critic paradigm in reinforcement learning. In RL, the agent is learning a strategy π to produce actions in a state s according to the distribution π(a|s), and the environment responds by providing the immediate reward r and the next state s’:

In a general policy gradient algorithm, π is learned directly from experience (as shown on the left). In an actor-critic architecture, there is a separate component within the agent that learns a value function, i.e., the expected total reward an agent would obtain starting from a state s, V(s), or starting from a state s with action a, Q(s, a); this is shown on the right above. A critic helps the agent to refine its policy updates.

With a learned world model, the actor-critic interaction becomes much richer: now the agent is able to “imagine” potential responses of the environment and search for whole sequences of actions, just like MuZero, but probably without the same kind of search tree since now the actions might be very numerous or even continuous. Here is a picture from (LeCun, 2022) that shows how a single episode of the agent interacting with the environment would go:

The sequence of actions here is entirely “in the mind” of the agent. Predicting a whole sequence of actions is probably quite expensive computationally, but once we have this prediction, we have a lot of loss function gradients to propagate: every step of the sequence can be compared with actual experience. So this approach can both help train better policies directly and also be used in a MuZero-like fashion to perform decision-time planning.

And with that, we come to our central point: what’s going on in OpenAI Sora?

Sora: A World Simulator or “Just” a Diffusion Model?

Ideas similar to Ha and Schmidhuber (2018) continue to define what world models mean for AI. The latest addition to the formidable OpenAI roster of foundational models, the state of the art video generation model Sora, is explicitly designed around the idea of world modeling. Their technical report is titled “Video generation models as world simulators”, although the report only states that Sora “simulate[s] some aspects of people, animals and environments from the physical world” and does not give any hard facts to support this, so we will have to make our own conclusions.

Following OpenAI’s recent (quite understandable) practice of limited transparency, there is no detailed paper on Sora, only a rather vague blog post and report. Essentially, the only thing that is clear is that it is based on a Diffusion Transformer (DiT). While we have discussed latent diffusion models on the blog before, and covered diffusion models in detail, but I have not yet explained DiT here, so let me provide some context.

Introduced by Peebles and Xie (2022), Diffusion Transformers showed that the Transformer architecture can be useful even for a denoising element of a diffusion model. For instance, Stable Diffusion (Rombach et al., 2022) used a diffusion model to produce the latent code for a VAE-based decoder, and DiT also follows the same basic structure (the picture is copied from a previous post):

However, this picture does not show what’s inside the denoising blocks. Stable Diffusion used a U-Net-like architecture with cross-attention layers that effectively utilized the condition, yet retained a general U-Net structure (picture from Rombach et al., 2022):

Diffusion Transformers use a “pure” Transformer block for denoising, with a neat trick of using the layer normalization block similarly to AdaIN (Huang, Belongie, 2017) style transfer blocks; illustration from (Peebles, Xie, 2022):

The resulting architecture proved to be much more compute-efficient than previously used U-Net-like diffusion models. In Sora, DiT is generalized to higher-dimensional patches that cover both space and time inside a video. Although the exact way it is done has not been revealed, there is at least one prior model, the GenTron by Meta researchers Chen et al. (2023), that adapts DiTs to video. Here is a generic illustration from the Sora report:

But I digress. Regardless of the model itself, Sora provides great video generation results that often exactly follow our intuitive understanding of physics, although sometimes they fail in that regard. Does this mean that Sora is at least halfway to the holy grail of learning an operational world model from raw video inputs?

At this point, let me link to a very detailed blog post by Raphaël Millière called “Are Video Generation Models World Simulators?”. It covers many of the points that we are going through here, and I recommend it in its entirety. In particular, Dr. Millière considers several definitions of a “world model” and carefully studies whether Sora is likely to fit any of them. His conclusions, which I fully endorse, are as follows:

• being a single end-to-end model that operates fully in latent space, Sora does not have separate components needed to actually have an “internal physics engine”, so it cannot be a “world simulator” in the sense of synthetic data simulators like MuJoCo;
• however, the structure of its latent space may well be sufficiently complex to capture and predict certain physical phenomena based on its latent representations.

To me, this is an interesting discussion (and a great post, please do read it!) but these conclusions slightly miss the point. Of course a deep learning model does not have an internal physics engine unless one is artificially attached to it (see below). You and I, however, may not have one either!

Again, I can only recommend reading through the section by Dr. Millière on “intuitive physics”: human infants learn to expect certain physical properties very quickly, and there is a well-established “IPE hypothesis” that posits the existence of an “intuitive physics engine” in our minds. But even for humans, it’s just a hypothesis, and there is an opposite opinion that human physical reasoning is based on visual shortcuts and generally predicting what we will see next rather than approximating the relevant laws of physics.

For Sora and similar models, this hypothetical intuitive engine is even harder to believe in. Some examples generated by Sora clearly violate even our basic intuitions like object permanence or collision properties, which is, of course, expected from a diffusion-based generative model, but not really expected from a physics simulator, however “approximate” it is:

The question for me here is: does it really matter? We humans probably don’t have a built-in Unreal Engine to tell us how the world works. But we have an intuitive understanding of the world that allows us to make predictions, and these predictions are accurate enough for most practical purposes. Sora is not quite there yet, but if some upcoming Sora 2 or Sora 3 does have a similar understanding, it will be enough to disallow videos with such internal contradictions. 

Still, this may sound like a lot of work for naught. Why should we wait until some latent representation learns to approximate Unreal Engine 5 from scratch when we already have Unreal Engine 5? Indeed, there have been attempts to combine machine learning models with external tool calls to world simulators; let’s discuss them before we conclude the post.

Adding a “true” world simulator: grounded LLMs

Even with all the RLHF fine-tuning and other advanced techniques, large language models primarily train as their name suggests: by predicting the next token of text. By default, they don’t have access to external tools like calculators or physics engines, and learning exclusively from text can lead to simple mistakes in this context.

In other words, a large language model, no matter how smart, is akin to a medieval scholastic thinker who derives knowledge exclusively from Aristotle but cannot conduct experiments or use empirical evidence. It would make a lot of sense to let an LLM call some external tools that would provide this evidence to use in the LLM’s reasoning and to inform its replies. This is called grounding, and it is indeed known to be a good way to improve LLM results:

For example, one significant result along this way was the Toolformer approach (Schick et al., 2023), where an LLM learns to use a new tool from a brief description of its API. As a result, the LLM can access a wide variety of tools and learn new ones on the fly (examples from Schick et al., 2023):

And yes, there already exist approaches that ground LLMs with “more real” world simulators to help them reason about our physical three-dimensional world.

For example, the recently developed Grounded 3D-LLM (Chen et al., May 2024) adds special referent tokens that correspond to objects in the 3D environment where the LLM is planning some actions:

Its 3D point cloud encoder is trained with a cross-modal pretraining procedure based on contrastive losses, similar to CLIP (OpenAI, 2021; see also our earlier post), and the LLM is fine-tuned with LoRA to understand how to work with referent tokens:

The work nearest to our current discussion was done by Liu et al. (2023) from Google Research. They recognize the problem of linguistic reasoning in the physical world and develop an approach called Mind’s Eye that lets an LLM to query a computational physical engine, in this case DeepMind’s MuJoCo (Todorov et al., 2012). 

The LLM writes rendering code and runs the external physics engine, informing its output with simulation results:

The authors show that this kind of grounding does help LLMs reason better with this “mind’s eye” powered by a computer simulation. So in a way, we already know how to insert a realistic externally implemented world model into an LLM to inform its reasoning about the world. Still, there are at least two important missing pieces:

• first, tool use in LLMs still leaves quite a lot to be desired; it is an active area of research where Toolformer has already been succeeded my many works (see, e.g., Tang et al., 2023; Qin et al., 2023; Zhuang et al., 2023), and there appears to be still some way to go before grounded LLMs reach maturity;
• second, even if this interaction between an external world model and an LLM worked perfectly, it would be quite far from physics-aware video generation: in this section, we are talking about specifying queries for the simulator and running experiments with simulated physics, but even if any videos do come out of it, they will be limited by the simulator’s capabilities.

In my opinion, a foundational model cannot practically run a complicated external tool every time it needs to generate something, but it can certainly use an external simulator for training. Software libraries such as MuJoCo can provide a foundational model, be it an LLM or a multimodal generation tool, with an endless stream of synthetic data and, more importantly, synthetic environments that could be used to experiment and learn about the physical world. This, again, brings us back to our favorite domain of synthetic data, which would include a synthetic physics simulator as well.

Conclusion

In this post, we have discussed world models in modern AI, starting from a very abstract notion of a world model and gradually making it more explicit until, in the end, we showed how to add an external physics-based simulator engine to state of the art LLMs.

I would like to conclude this post by mentioning a recent work that appeared in May 2024: a paper by MIT researchers Huh et al., titled “The Platonic Representation Hypothesis”. In agreement with Plato’s ideal world of perfect forms (eidos), the authors posit that sufficiently expressive neural networks will converge to the same “optimal” representation of reality in their latent spaces, regardless of the modality they are trained on. This hypothesis is supported by several observations and empirical evidence in this intriguing work:

Still, despite the appearance of Sora that is head and shoulders above previously existing video generation models, and despite recent models that model visual environments with diffusion models and ground LLMs with interactive physics simulators, it looks like the field of applying world models to modern generative AI is still at its very inception. It will be exciting to see how world models become better and more prominent across various AI-related domains, and here at Synthesis AI we hope to spearhead at least some of these applications. See you next time!

Sergey Nikolenko
Head of AI, Synthesis AI

The announcement of Gemini 1.5 by Google was all but eclipsed by OpenAI’s video generation model Sora. Still, there was one very important thing there: the promise of processing a context window of up to 1 million tokens. A very recent announcement of new Claude models by Antropic also boasts context windows of up to 1M tokens, with 200K tokens available at launch. Today, we discuss what context windows are, why they are a constraint for Transformer-based models, how researchers have been trying to extend the context windows of modern LLMs, and how we can understand if a large context window usefully works. By virtue of nominative determinism, this is a a very long post even by the standards of this blog, so brace yourself and let’s go!

The Quadratic Complexity of Self-Attention

One of my last posts was intended to provide detailed background on the Transformer architecture based on the original “Attention is All You Need” paper, so I will not repeat the introduction again. All we need now (pardon the pun) is to recall how self-attention itself works in general terms; here is a picture from that background post:

There is an important problem here that follows from the very structure of self-attention. The formula that everyone has been copying thousands of times looks as follows:

   

The matrix computation inside the softmax is what matters most for us today. To get to the final result we need to compute self-attention weights between every pair of input tokens

   

which means that we need to get a result of size , quadratic in the number of input tokens. 

This is in fact a tradeoff that self-attention brings to the table compared to, say, recurrent networks. An RNN can read its input in linear time, where  is the input dimension, because it reads the input consecutively, token by token. But this means that to get from token 1 to token L you have to make L steps, one by one. This is why RNNs struggle with long-term dependencies: the influence of a token gets diluted and reduced as you make way through the intermediate sequence. A lot of what has been happening in RNNs, including LSTM and GRU recurrent units, has been designed specifically to alleviate this problem. In a Transformer, the problem just vanishes: you get from any token to any other in a single step—at the cost of quadratic complexity of the layer.

Unfortunately, quadratic complexity of self-attention is not some intermediate result that you can hope to optimize away by designing a more efficient algorithm. The actual number of weights is quadratic, and while there may exist faster approximations (we will discuss them below), we cannot get it entirely right in subquadratic time.

Actually, there even exist negative complexity theoretic results proven by Keles et al. (2022) who provide a kind of “no free lunch” theorem for self-attention. Specifically, Keles et al. prove that:

• you cannot get sub-quadratic algorithms that compute self-attention exactly unless you can solve NP-hard problems in subexponential time (this is known as SETH, the Strong Exponential Time Hypothesis, and it is just as widely believed to be true as the P!=NP assumption that it strengthens);
• moreover, under the same assumption you cannot even get a subquadratic algorithm that approximates all attention weights up to a constant, either an additive constant or a multiplicative one.

Here is a summary table from the paper where checkmarks correspond to proven negative results; as you can see, some additive approximations are still possible but overall it looks pretty comprehensive:

Quadratic complexity does not look like an obstacle as insurmountable as the exponential complexity of NP-hard problems. It may sound like a lot of commonly used algorithms have quadratic complexity. For example, bubble sort has complexity in the worst case and even long multiplication of two n-bit numbers has quadratic complexity (quadratic in total input size, of course, which is logarithmic in the values of the numbers themselves).

But this is an illusion: for common problems such as sorting and multiplication, naive algorithms may be quadratic but as soon as you want to scale them up to large arrays and really large numbers, you have to find something more efficient. There are plenty of algorithms for sorting. Multiplication has been done with Karatsuba’s algorithm in time since the 1960s, and a recent highly acclaimed result by Harvey and van der Hoeven (2021) has brought integer multiplication down to the same complexity (although the algorithm itself is probably too involved to find much practical use). In fact, you would be hard pressed to find practical problems that actually have quadratic complexity that people don’t know how to reduce further. In this regard, computing self-attention is actually an important example for theoretical computer science as well.

Authors of the original Transformer did not yet have the negative theoretical results but they already understood that quadratic complexity is hard to scale. They remark on the quadratic complexity of self-attention throughout the paper and even propose a middle ground solution that can alleviate it. Let us call it the sliding window attention: it restricts the self-attention mechanism to a subwindow of size r around the current token. Then

• instead of , where  is the embedding dimension, the self-attention layer will only have complexity since now we compute only r attention weights around each of L input tokens;
• but the tradeoff is that now we cannot get from any token to any other in a single step, we have to make sequential steps from one side of the input sequence to the other.

Despite promising results in the original paper, this solution has not really caught on; I believe that it sacrifices too much to be useful, working too much like an RNN as a result. But increasing context size has remained one of the central problems for Transformer-based architectures ever since they were first designed in 2017. In the rest of this post, we will discuss other ways to reduce the complexity of self-attention.

Sparse Attention Mechanisms: Do We Need the Full Square?

The first obvious research idea here goes like this: okay, suppose we do have to have quadratic complexity to compute a quadratic number of attention weights, but do we really need all these weights? The sliding window attention from the original “Attention is All You Need” paper falls into this category as well, but more successful approaches were developed later.

In 2020, researchers from the Allen Institute of AI Beltagy et al. proposed Longformer, a replacement for the full-scale quadratic attention mechanism that scales linearly with input size. The basic idea is to still use the sliding window attention—after all, local context is indeed usually the most important—but augment it with several important tricks. Here is a general illustration from the paper:

The first trick here, shown in part (c), is to use a dilated sliding window that skips over some inputs, using, say, every second one. This idea is well known in convolutional architectures, where it is also used to increase the receptive field of neurons, covering more ground in fewer layers. In the one-dimensional context it was very successfully used, say, in the WaveNet architecture; the illustration of WaveNet shown below explains how repeated dilation can exponentially increase the receptive field, which in our case means reducing the number of steps needed to go over the entire input:

Moreover, in Transformer’s multi-head self-attention you can use different dilations for different heads! For example, if the first head uses odd-numbered tokens from the input, and the second head uses even-numbered tokens, the window size doubles with the same number of attention weights but the layer does not skip anything from the input.

The second trick, shown in part (d) above, is to have several tokens that have global attention so that their weights span the whole input. Now for every token with global attention you have O(L) attention weights but the assumption is that there are only a constant or logarithmic number of such tokens so the overall number of attention weights remains low. 

This trick is well known to anyone who has used, say, BERT embeddings in practice: it is usually very helpful to add a special [CLS] token and use it to capture global properties of the input, e.g., train a classifier on [CLS] embeddings. This is exactly the function of global attention in Longformer, only now we remove most of the attention weights between other tokens.

Longformer proved to be quite efficient in practice, but there also exist some conceptually more interesting ways to implement sparse attention. In “Generating Long Sequences with Sparse Transformers”, four OpenAI researchers (Rewon Child, Scott Gray, Alec Radford, and Ilya Sutskever) studied the attention patterns learned by full quadratic self-attention layers and found that most layers had sparse attention patterns. Therefore, they proposed to formally restrict self-attention to sparse patterns: each attention head i has a subset of input tokens that it attends to. At the same time, Child et al. require that the factorization into is valid, i.e., that every token can attend to every other in p attention steps. 

It turns out that one can choose efficient factorizations , finding valid of size , which is obviously minimal since you need to get to L in p steps. Specifically, they build upon the natural general idea for such a factorization: one head attends to l sequential locations, and the other head uses a kind of dilated sliding window with stride l, where l is close to .

There are two basic ways to implement this; in part (b) of the figure below dilated attention moves along the tokens, and in part (c) there are selected positions that a lot of other tokens attend to, but a composition of such two heads (light blue and dark blue) connects every pair of tokens in both cases:

Child et al. comment that the first kind of sparse decomposition (part (b) of the figure) works well for data with periodic structure such as images or music, while fixed attention patterns (part (c) of the figure) are better for data without clear periodicity, such as text. They also make use of an earlier OpenAI development: block-sparse weight matrices implemented at the hardware level, as GPU kernels (Gray, Radford, Kingma, 2017); this allows to make sparse self-attention matrices very efficient in practice.

The last paper I want to mention in this section is “Big Bird: Transformers for Longer Sequences” by Google researchers Zaheer et al. The structure of their sparse self-attention mechanism combines previously developed ideas: global tokens that attend to everything, sliding windows that attend to local context, and a set of random attention weight positions that add expressivity at a small computational cost:

They view self-attention as a directed graph that shows which positions attend to which other positions; the figures we have seen in this section are adjacency matrices for such graphs. Under this view, the requirement that every token can attend to any other in a few layers turns into the requirement that the adjacency graph has short paths between the nodes. Fortunately, random graphs do have that property. Zaheer et al. consider two random graph constructions:

• in the Erdős–Rényi model, every edge is chosen at random with a fixed probability; it is known that in this model, shortest paths have on average logarithmic length, which would suit us fine, but the Erdős–Rényi model does not have another important feature: locality, i.e., in this approach a token will not attend to the local context around it;
• therefore, Zaheer et al. move on to the Watts–Strogatz model that begins with a ring lattice (where every token attends to a fixed size window around itself) and then adds random connections; this can achieve a good balance between shortest path lengths and local context;
• finally, the Big Bird model also adds global tokens, as described above (and as shown in the figure above).

In summary, in this section we have discussed several approaches that reduce the number of weights by decomposing the full attention matrix into a composition (product) of several sparse matrices. We have viewed it as a sparse graph where it takes several steps to go from one vertex to another, or you can view it in a way similar to dilated convolutions with added global tokens. But there is another way to arrive at a similar approach: sparse matrix decompositions; let us consider it separately.

Low-Rank Decompositions: Linformer and Performer

Another direction from which we can attack the quadratic complexity is to use low-rank approximations and/or projections to reduce the size of the matrices. This is a very important and useful trick: if you have a huge matrix X that you cannot really work with, you can try to reduce it by decomposing X into a product of two rectangular matrices, one of size (denoted U below) and another or size (denoted V):

The actual mathematical result, called the singular value decomposition (SVD), says that you can do it if X has rank at most k, but even if not, you can consider a low-rank approximation to X in this form. For example, recommender systems make use of the SVD all the time. In a recommender system:

• X is the matrix of ratings (or likes, or any kind of user responses), where N is the number of users and M is the number of items, and most values of X are unknown (a user has surely rated only a small subset of items);
• U is the matrix of user features, i.e., dense numerical vectors of size k that describe every user; V is a similar matrix of item features;
• and if we find a good low-rank approximation UV for known elements of X, it will allow us to give predictions for unknown elements of X by taking the dot product of user and item features (that’s exactly what’s happening in matrix multiplication).

So how does this idea help reduce the complexity of self-attention? We will consider two variations of it.

First, the Linformer architecture, proposed by Facebook AI researchers Wang et al. (2020), is probably the most straightforward way to apply low-rank approximations to self-attention. The authors begin by noting that self-attention matrices in practice usually have low rank:

The plots on the left show that the 128th eigenvalue (out of embedding size 512) already captures most of the information in the self-attention matrix, and the plot on the right, which shows the share of shows cumulative eigenvalues is taken by the first 128 out of 512, indicates that this effect is more pronounced in higher layers. The authors even provide a theoretical justification for this, which we will not go into.

What this means is that we can replace the self-attention matrix with a low-rank approximation. To do that, we need to add a projection matrix after the key and value matrices, projecting the context window size n down to some smaller value k:

The query matrix remains of size , and we get a formula for self-attention where there are plenty of matrices but no matrices:

   

where and are  projection matrices, so the outer product is a product of an matrix of attention weights and a  projected matrix of values.

As a result, the Linformer does scale very well with the input sequence length, as shown in the top right plot above. But there are other ways to apply similar ideas too.

The Performer architecture, developed in a collaboration between Google, Cambridge, DeepMind, and Alan Turing Institute researchers (Choromanski et al., 2021), introduces the Fast Attention Via positive Orthogonal Random features approach (FAVOR+) based on a low-rank decomposition with random features. Let’s dive into some details here.

We know that in a self-attention layer, the Transformer uses an attention weight matrix A to create convex combinations of the value vectors V. Moreover, as we know, A is in fact produced by passing the matrix of (normalized) dot products between query and key vectors through the softmax function:

   

FAVOR+ generalizes this construction as follows: let us consider arbitrary matrices produced as

   

where is a kernel function . For Transformer self-attention, is the softmax function of the scalar product normalized by . 

Suppose that we can construct a randomized mapping (random feature map) such that maps the input embedding into some smaller space of dimension , , and in expectation gives us the kernel function:

   

If we can find such a random feature map , it will give us a natural way to approximate the attention mechanism: 

• map the embeddings into a smaller r-dimensional space via and represent the computation of attention weights as above;
• but then compute the product of the new key matrix and the value matrix before multiplying by on the left; in this way, we never compute an matrix but instead compute an  matrix of dot products of vectors of length and then multiply it by an matrix on the left.

Here is what it looks like; and are and respectively:

Choromanski et al. consider several different ways to define the random features, and even provide theoretical results that show how positive orthogonal random features can lead to good approximations for the softmax kernel used in regular self-attention.

In summary, low-rank decompositions provide another very efficient way to cut down on the quadratic complexity: they allow to never consider the full  matrix for a large  but instead always deal only with projection  matrices and dense  matrices in the reduced dimension. In the next section, we will consider a couple of ideas that are different and do not fall neatly into the categories of either sparse attention or low-rank decompositions.

Chunking the Attention: GAU, MEGA, and Reformer

The last set of ideas I want to discuss is a direction that, surprisingly, has not yet appeared in this post: what if we just tweak the network architecture of self-attention? Usually that would mean that the quadratic complexity of attention remains in place, but is constrained to small subsets of the input, and these small subsets (chunks) are connected to each other in some additional way. In this section, we consider different ways to do that.

As the first representative example of this direction, let us discuss the Gated Attention Unit (GAU; Hua et al., 2022), a variation of GRU with an attention mechanism. It also invites us to have a different look on some of the matrix calculations we have already seen.

But first let us describe the GAU itself. It combines the familiar multi-head self-attention mechanism with the gated linear unit (GLU) shown on the left of this figure (Hua et al., 2022):

A gated linear unit applies two dense transformations to the input and multiplies them componenwise, in effect gating the obtained representations with each other (recall, e.g., how LSTMs work: they use gating mechanisms a lot).

So the Gated Attention Unit (GAU), as shown on the right of the figure above, combines a GLU and regular multi-head self-attention, sharing the computations of these layers: basically it is a GLU where one of the representations is also multiplied by the matrix of attention weights from other elements in the sequence, computed as the usual . Hua et al. show that after this modification, you can replace softmax with ReLU and also simplify the computation of Q and K matrices; please see the paper for more details.

Still, GAU is quadratic in the input size! But it will lend itself better to the chunking approximation that follows. We know that self-attention is quadratic as written:

   

But if we forget about the softmax and try to approximate this attention mechanism with QK^TV, we can rearrange the terms:

   

Now the matrix in brackets is a matrix, and there is no quadratic dependency on the input length . Moreover, we can compute the matrix incrementally, step by step: for every new input at time ,

   

and we can just store its value in a cache of size and add new values as they arrive. Here is how Hua et al. illustrate this; the left side of the picture above contrasts quadratic attention and linear attention:

This linear attention is similar to the attention mechanisms used in RNNs. Hua et al. try to have the best of both worlds: they split the input into chunks and use quadratic local attention inside each chunk, just like regular GAU, and linear global attention between chunks, as shown on the right of the figure above. As a result, they report results very similar to the basic Transformer self-attention with much less complexity.

GAU has found applications in speech analysis (Tsai, Khoa, 2023) and has been combined with convolutional networks such as U-Net to improve image segmentation (Wang et al., 2023). Next, we consider one more detailed example of how GAUs have been used and modified.

Building on GAU, a collaboration of Carnegie Mellon, USC, and Meta AI researchers presented the Moving Average Equipped Gated Attention, or MEGA (Ma et al. 2022). Unfortunately, this paper is not yet among the top results for the “Mega Transformer” Google search, but here’s hoping that citations will accumulate.

MEGA is based on the idea of an exponential moving average. Suppose that you want to smooth out a series of numbers so that every resulting number is influenced by several past values in the series. You could take an average over a sliding window, and it would probably give the desired effect, but there is an important disadvantage: you will have to keep the entire window in memory; otherwise you won’t be able to subtract the values that come out of the window as it slides.

If you need to save memory, you want to change the semantics and instead of a sliding window use an update rule like this:

   

If you unroll this formula to previous steps, you will see that the exponential moving average gets a theoretically infinitely long memory with exponentially decaying weights of the inputs, hence the “exponential”; here is an illustration from Ma et al. (2022):

The weight  controls how long you want this memory to be. This is a classical trick known for centuries, so how do we apply it to the Transformer architecture? Here is the general overview from Ma et al. (2022):

As you can see in (a), the basic Transformer architecture remains in place, but the self-attention layer is replaced with a “Mega layer”. The idea of this layer, shown in (b), is as follows:

• first, the input sequence , which is an matrix, is expanded into  dimensions via a expansion matrix :

     

• second, EMA is applied to the expanded matrix ; note that the Mega architecture uses what they call damped EMA, where the influence of previous steps is reduced by the damping factor :

     

• third, the result is projected back with an d⨉h projection matrix :

     

But wait, this looks nothing like figure (b) above! Indeed, this is all hidden between the “Layer input” and “EMA output”. The important part of figure (b) is what happens with the result, and this is where recurrent networks come into play. 

MEGA uses the Gated Recurrent Unit (GRU; Cho et al., 2014), a standard recurrent architecture developed as a simplification of LSTM, and the Gated Attention Unit that we discussed above. I will not go into too much detail about them, but basically GAU is the attention unit shown in figure (c) above, and then the results are processed as a sequence with the GRU unit as shown in figure (b).

Interestingly, we have not yet done anything with quadratic complexity! The architecture above introduces a stronger inductive bias into the attention mechanism, i.e., makes it more position-sensitive. After doing that, MEGA can simply break the modified attention mechanism into chunks with quadratic attention applied to local segments, and connections between chunks supported in particular through the exponential moving average mechanism:

So the actual reduction of quadratic complexity is very simple here, although different from the basic GAU: in GAU, information flows between quadratic chunks in a linear RNN-like style, while here we have a more complex (and hopefully more informative) relationship supported by the exponential moving average.

But recurrent connections between sequential blocks are not the only way to chunk the input. Our final idea, called the Reformer, comes from Google Research (Kitaev et al., 2020). The Reformer actually introduces several interesting tricks to improve the performance of a Transformer, including reversible layers from Gomez et al. (2017) that allow to store only a single copy of activations in the model and splitting activations in feedforward layers that further saves memory.

But we are interested specifically in what they propose to alleviate the quadratic complexity of self-attention. For that, Gomez et al. go back to the self-attention formula that we started with:

   

Note that we are not really interested in the actual values of the matrix , only in , and the results of a softmax function are dominated by a few largest elements, while the smaller elements have negligible influence on the result. If we have something like 64000 different keys, for each query  it would be enough to consider only 32 or 64 keys  nearest to  in the embedding space. How do we find these nearest neighbors?

Finding nearest neighbors is hard in the worst case, but there is a well-known trick in computer science called locality-sensitive hashing (LSH; see, e.g., Wikipedia and references therein): we can get a very efficient approximate algorithm for finding nearest neighbors if we can find a hash function h(x) that assigns nearby vectors to the same bucket with high probability.

In a Euclidean space of embeddings, such a hash function can be given by random projections: let’s fix a random matrix that projects x to a much lower dimension and then define the hash as a set of buckets that values on different axes in that lower dimensional space fall into. In the illustration below (Gomez et al., 2017), the points are projected onto a sphere (circle), then the points are randomly rotated, and the hash is defined by the set of indices of the segments (there are four colored segments in the figure) where a point falls after these rotations:

After hashing, we can look for nearest neighbors only in the current hash bucket, and with high probability we will not miss anything. For self-attention, this means that we restrict the attention matrices to a given hash bucket; the general scheme is as follows (Gomez et al., 2017):

This trick will only work if we are actually looking for nearest neighbors rather than doing generic retrieval, i.e., only if Q=K. Interestingly, this restriction does not lead to any significant loss of quality! Gomez et al. compare this “shared-QK attention”, where the weight matrices for keys and queries are fixed to be equal, with regular Transformers and find negligible difference in performance.

Other ideas and research directions

By now, we have discussed all the primary classes of methods one can try to increase the context window size: sparse attention, low-rank decompositions, and chunking the input via architectural modifications. For the detailed discussion above, I chose methods that keep the basic idea of self-attention rather than replace it with something else entirely, but there are plenty more approaches, of course. Here are a few of the most notable that we have not had time to consider in detail.

First, FlashAttention (Dao et al., 2022) makes self-attention IO-aware and dives into the hardware specifics, using tiling to reduce the number of read/write operations between GPU high-bandwidth memory and GPU on-chip SRAM:

It has been a big success and has already been further developed by the author into FlashAttention 2 (Dao, 2023).

Second, there are several block-wise approaches, that is, approaches that break down the quadratic matrix multiplication into a composition of multiplications of smaller matrices; just like MEGA did with its chunks. In particular, MEGABYTE (Yu et al., 2023) stacks two Transformers together, one for patch embeddings and another for individual tokens inside the patches, while blockwise parallel Transformers (Liu, Abbeel, 2023) put parallel blocks inside the self-attention mechanism itself. In the picture below, I combined the illustrations from these two papers:

Third, attention-free Transformers (AFT) replace multiplication of the query and key matrices with learnable position biases added to the key matrix. Then the query matrix is just multiplied componentwise to the result, sidestepping quadratic complexity entirely. The idea of AFT started with Apple researchers Zhai et al. (2021); here is their illustration of the new attention mechanism:

Finally, MEGA combined self-attention with recurrent networks, but there is also a direction of research that just try to improve RNNs themselves. Katharopoulos et al. (2020) introduced fast autoregressive Transformers based on RNNs with linear attention. Gu et al. (2022) developed the Structured State Space (S4) sequence model based on recurrent state space models, and it was further improved in diagonal state spaces (Gupta et al., 2022, Gu et al., 2022), gated state spaces (Mehta et al., 2022), and selective state spaces (Gu, Dao, 2023).

A large context size was achieved with an architecture reminiscent of the Transformer but with linear recurrent units stacked instead of self-attention layers (Orvieto et al., 2023); here is their main illustration that combines all the pieces:

In a different line of RNN research, the receptance weighted key value (RWKV) architecture presented by a huge collaboration of researchers from nearly 30 different institutions (Peng et al., 2023) also promises to “reinvent RNNs for the Transformer era”.

Each of these items could easily warrant a blog post of its own, and I can refer to a couple of full-scale surveys already devoted to the topic (Tay et al., 2022; Ding et al., 2023; Xu et al., 2024). But for us, it is time to move from possible answers back to the question itself: once you have an architecture that is supposedly ready to process long context windows, how do you test that?

Testing Long Context: Needles and Haystacks

In the last two sections, we ask another fundamental question: suppose we have used one idea or another to process a huge number of tokens at once. But how can we understand whether a LLM actually processes its long context window meaningfully rather than skip most of it? One standard test is to ask the model to look for a needle in a haystack: we fill the context window with either meaningless or random stuff and insert a single fact that the model later will have to fish out.

As far as I know, one of the first iterations of this idea was released about a year ago in the Little Retrieval Test (LRT) by researchers from the University of Wisconsin-Madison and Yongsei University. It has a very simple structure, with meaningless numbers as filler information and a single line that instructs the model to go to a specific line and report its content:

line 1: REGISTER_CONTENT is <2156>
line 2: REGISTER_CONTENT is <9805>
[EXECUTE THIS]: Go to line 5 and report only REGISTER_CONTENT, without any context or additional text, just the number, then EXIT
line 3: REGISTER_CONTENT is <6668>
line 4: REGISTER_CONTENT is <1432>
line 5: REGISTER_CONTENT is <6727>
line 6: REGISTER_CONTENT is <3936>
line 7: REGISTER_CONTENT is <1805>
line 8: REGISTER_CONTENT is <431>
line 9: REGISTER_CONTENT is <1720>
line 10: REGISTER_CONTENT is <6794>

In a harder version, the lines are shuffled randomly. LRT was designed at the time when GPT-4 and Claude appeared, boasting long context windows. The results did support Claude 1.3’s claim for processing long context, up to 100K tokens which means about 6500 lines in LRT:

In the end of June 2023, the LongChat team took the LRT and ran with it, making “fluff” information a little more meaningful for LLMs by replacing numbers with random text:

line torpid-kid: REGISTER_CONTENT is <24169>
line moaning-conversation: REGISTER_CONTENT is <10310>
…
line tacit-colonial: REGISTER_CONTENT is <14564>What is the <REGISTER_CONTENT> in line moaning-conversation?

The results again showed Claude 1.3 and GPT-3.5-Turbo coming out on top:

The next step came in Greg Kamradt’s “Needle In A Haystack” test released in November 2023. He changed the “haystack” to real meaningful text, and the overall process became as follows:

• take Paul Graham essays as the input context; Kamradt used 218 essays with about 200K tokens, repeating the essays to make the input longer;
• use a random but still meaningful statement as the “needle” to be found; Kamradt’s example was: “The best thing to do in San Francisco is eat a sandwich and sit in Dolores Park on a sunny day”;
• ask the LLM to answer this question only using the context provided, and evaluate the answer with GPT-4 using LangChain evals (let’s not go into that further, here it basically means asking GPT-4 if the “needle” was found correctly).

The results were nontrivial: even in the claimed context windows, retrieval accuracy degraded significantly as the “needle” fact was placed deeper in the context window. Here are the results for GPT-4:

And here is the plot for Claude 2.1 available in November 2023:

Greg Kamradt’s test became very popular; for example, the Gemini 1.5 Pro release I started this post with links to NIAH evaluation and claims to find the needle 99% of the time in input blocks “as long as 1 million tokens”. Here is the results plot Google shared in their Gemini 1.5 technical report:

This is only the text part; the multimodal results are even more impressive, and I hope to get back to multimodality in subsequent posts.

Now comes a little twist about this kind of testing. We saw that the original LRT used random numbers as facts for both “needle” and “haystack”. Later iterations of the test became more and more meaningful, with Greg Kamradt using coherent essays and “hiding” a subjective but plausibly sounding fact about San Francisco. But lately, researchers have gone back to meaningless information. Gemini 1.5 uses “needle” facts of the form “The special magic {random_city} number is: {random_number}”, and the task is to retrieve this number by the city name. Google researchers refer to recent work by Arize.ai which is basically Kamradt’s test with this change, so in a way we have come full circle back to the original LRT. I think it might be interesting to compare how (and whether) the “meaningfulness” of hidden information influences the results.

I will close this section with one last result that sounds very interesting to me. Claude 3 Opus, an LLM just released by Antropic, was also tested with “needle in a haystack” type tests. In some cases, it actually managed to not only find the “needle” but also notice that it is probably being evaluated! Here is a sample output reported by Antropic researcher Alex Albert:

Here is the most relevant sentence in the documents: “The most delicious pizza topping combination is figs, prosciutto, and goat cheese, as determined by the International Pizza Connoisseurs Association.” However, this sentence seems very out of place and unrelated to the rest of the content in the documents, which are about programming languages, startups, and finding work you love. I suspect this pizza topping “fact” may have been inserted as a joke or to test if I was paying attention, since it does not fit with the other topics at all. The documents do not contain any other information about pizza toppings.

Is this yet another sign of AGI coming soon? I don’t know, but it sure looks like one…

Kalamang to English: Machine Translation from One Book

LRT-style tests are informative but relatively bland. But there is a test for (very) long context windows that totally blew my mind when I first heard about it.

Meet Kalamang, a language spoken by less than 150 people in Papua New Guinea, a well-known repository of rare languages thanks to its structure of isolated islands (linguists estimate 840 languages—complete languages, not dialects!—spoken in this country with a total population of under 12 million). The Endangered Language Project ranks Kalamang as “Severely endangered”, remarking that “no one born after 1990 can be counted as a fluent speaker, and it is rare for them to have two fluent Kalamang-speaking parents”.

In 2020, Eline Visser, a researcher from Lund University in Sweden, published her Ph.D. thesis in the form of a book called “A Grammar of Kalamang: The Papuan language of the Karas Islands”:

It is a classical linguistic work that systematically describes the Kalamang language, complete with phonetics, morphology, word classes and so on, complete with English-Kalamang and Kalamang-English wordlists and a small sample of parallel translations.

Since Kalamang is an oral language spoken by so few people, we can safely assume that Eline Visser’s book is the only resource publicly available for this language. This has led to the idea implemented by a team of researchers including Eline Visser herself: Tanzer et al. (2023) turned the Kalamang language into a testbed for LLMs.

We all know that large language models are able to translate between languages; just ask ChatGPT and see for yourself. But it is one thing to translate from French to English, where resources abound in both languages, including a wide range of language primers, parallel texts, vocabularies and the like, and quite another to translate from Kalamang that only has one book about it, period.

So in the original paper, Tanzer et al. found that machine translation from one book (MTOB) is indeed a very hard benchmark. Naturally, LLMs have zero prior knowledge of Kalamang and all have basically random performance without context, but it is hard for LLMs to learn a new language even when given Visser’s book as context. Here is a qualitative sample from the paper; naturally, I do not understand Kalamang but I guess we can assume that human output is correct:

Note how LLMs that can write perfect English, even the almighty GPT-4, all have very awkward outputs that they themselves would definitely edit out of existence if asked. In fact, here is what GPT-4 told me about its own translation, probably straying further from the original but keeping the meaning of the translation just as I would understand it myself:

The test set produced by the authors is large enough to allow for quantitative comparisons. And right now, it is a perfect test for long context windows since they only very recently have become long enough to fit Visser’s book. 

The MTOB benchmark has been picked up by newer models: the Gemini 1.5 Pro report already includes a comparison table that boasts quantitative improvements and even shows that the full book context improves in comparison to half of the book, again highlighting how important it is to maximize the context window size:

Conclusion

Having a large context window has been one of the key obstacles to scaling up large language models to many real life applications. Since by default Transformer-based LLMs do not have persistent memory and cannot run algorithmic loops (they have a fixed, and not very large, number of layers), a LLM is limited in its reasoning to whatever it has memorized inside its weights and whatever fits into its context window. But the default self-attention layer that Transformers are based on has quadratic complexity in the length of its input sequence, making long context windows impractical.

In this (very long) post, we have discussed several different ways to overcome the quadratic complexity bottleneck of Transformers and thus extend the context window. We considered several main directions: sparse attention mechanisms that replace the full self-attention matrix with a sparse submatrix, low-rank decompositions that replace the same matrix with a product of smaller rectangular matrices, and different ways to break down the self-attention computation into blocks, including a mix of attention mechanisms and recurrent networks. We have also discussed how one can test that a context window is indeed large, and that the model can actually pick up all of the information from its context window.

In the next post, I will go back to the other big piece of AI news from the last month: the Sora video generation model and generally how modern Transformer-based architectures construct their world models. We will discuss what “world models” are, how they have progressed over the last few years, and what are the current obstacles that we still need to overcome. Until then!

Sergey Nikolenko
Head of AI, Synthesis AI

One of the most interesting AI-related news for me recently was a paper by DeepMind researchers that presented a new mathematical result found by large language models: new constructions for the cap set problem. In this post, we take a step back and discuss the general relation between math and AI. A mathematical proof is easy to verify but may be very hard to find. But there are AI-shaped holes in looking for a proof: math involves multi-step reasoning and planning, hard theorems need to be decomposed into lemmas, there are search strategies involved… However, mathematics has turned out to be unexpectedly difficult for AI. In this post we discuss what people have been doing with AI in math and how LLMs can help mathematicians right now.

Mathematical logic: formalizing the formal

I am a mathematician by education, and I have been doing math in some form or other throughout my career. My M.Sc. thesis in 2005 (almost 20 years ago! how time flies…) was devoted to structure theorems for Chevalley groups, my Ph.D. in 2009 was on theoretical cryptography where the main content is theorems rather than protocols, and my Sc.D. (habilitation) thesis in 2022 was devoted to the analysis of algorithms for networking and was also full of theorems.

The general workflow of a professional mathematician goes a little bit like this:

This is a big simplification, of course; for example, you often begin not with a problem but with a method, and try to find an interesting way to apply this method to some new application. But to a first approximation, solving a problem in mathematics usually means proving something, and when you try to prove something new, you usually need to come up with some creative ways to do it. Then your idea needs to be fully fleshed out: that’s where most ideas fail, and it’s back to the drawing board for the mathematician. Finally, once the proof is done, you need to verify it and, if everything is fine, write it up for publication.

I worked on mathematical logic, then machine learning and artificial intelligence, and through all these years I couldn’t help but wonder: why could I still be a mathematician? How is it possible that in our time, 100 years after Hilbert and 80 years after Gödel, theorems are still proven by live flesh and blood people? Let me elaborate a little so you can feel the wonder too.

Mathematics is the most formalized field of research; it is not a “science” since it does not deal with the dirty material world. Mathematics lives in a separate magisterium of abstractions where everything is absolute: you accept a few axioms and derive everything from these theorems via formal derivation rules. And by “formal”, I mean really formal, not general proof ideas like “reasoning by contradiction” but specific indisputable axioms that convert logical formulas to other logical formulas such as modus ponens: if we have a formula P and another formula P→Q, where → denoted implication, then we can add Q to our set of derived formulas (and use it further in the proof).

For example, Alfred Whitehead and Bertrand Russell (shown below) wrote a famous book called “Principia Mathematica”, where they attempted to build the whole mathematics from the ground up, starting from the axioms. In the book, the proof for 1+1=2 appears on page 379:

Naturally, that’s because they had to define the entire set theory, natural numbers, and addition first, but it is still quite an amazing piece of trivia.

Theoretically, you can write down the proof of every correct theorem as a formal chain of such derivations. It will be unbearably cumbersome, so I can’t even give you a serious example here, but in theory it can be done. More modern branches of mathematics such as group theory have this formalization built in: they start off with a fixed set of axioms (definition of a group in this case) and derive theorems formally.

Formalization is a relatively recent idea. For example, high school geometry is usually the place where you can get a feeling for mathematical proofs, but it is actually a pretty informal affair, with a lot of holes that Euclid did not fill. When mathematicians tried to patch up geometry, the 5 Euclid’s axioms expanded into 16 for Hilbert or 10 for Tarski (plus an extra axiom schema). Calculus was initially a rather intuitive affair, tightly interwoven with physics, differential equations, and practical applications. The derivative is the speed, the second derivative is the acceleration, and so on. It was only in the XIX century when all those suspicious counterexamples you vaguely recall from calculus classes (such as the Dirichlet function which is 1 on rational numbers and 0 on irrational ones) finally caught up with mathematicians and made “intuitive math” no longer viable. Something was wrong: mathematics needed to fix its foundations.

The answer was to introduce formal axioms and derivation rules and make math purely formal; this was the project initiated by Georg Cantor and Gottlob Frege in the second half of the XIX century and almost completed by David Hilbert in the beginning of the XX century. In this project, mathematics begins with set theory, usually introduced with Zermelo-Fraenkel’s axioms, and then other branches of mathematics are defined in terms of sets. For instance, natural numbers are usually introduced as ordinals: 0 is the empty set, 1 is the set with one element which is the empty set, {∅}, 2 is the set {0, 1} = {∅, {∅}}, 3 = {0, 1, 2} = {∅, {∅}, {∅, {∅}}}, and so on.

I say “almost completed” because Kurt Gödel’s incompleteness theorems proved to be an unfixable flaw in the original Hilbert’s program: for any reasonably powerful proof system (sufficiently powerful that it can include arithmetic), you can find true statements that are nevertheless unprovable. When Hilbert heard about these results, he went through all five stages of grief, from anger to acceptance.

But really, Gödel’s incompleteness is not a problem in practice. Sure, there exist true unprovable statements, and there is a whole cottage industry devoted to finding specific unprovable statements (wiki). But you won’t find them in everyday mathematical practice. If you want to prove a new theorem, you can be quite certain that it can be proven within “standard mathematics”. Even if a notable counterexample arises (can the Riemann hypothesis be undecidable?), it will remain just that: a very, very special case.

So we can safely assume that formal proofs of new, unproven theorems exist somewhere in the abstract world of mathematical absolute. The next question is: how do we find them?

Automated theorem proving and early AI

Formal proofs are hard to find, but once a proof has been found, it is easy to check that all derivation rules have been applied correctly. You could say that finding proofs for theorems is in NP (recall the P=NP problem)… if you measured complexity as a function of the size of the proof rather than the theorem itself. The problem is that some proofs may be unbelievably large, far exceeding the number of atoms in the known universe even for a small and obviously true statement (alas, it would get too technical to give specific examples).

Proof size depends on two things: the statement (theorem) that’s being proved and the proof system where it’s happening, i.e., which axioms and derivation rules we are allowed to use. Universe-sized counterexamples could be proven very compactly, even elegantly in more powerful proof systems — otherwise how would we know they are true? But there is an inherent tension here between the size of the proof and the expressive power of the proof system. You can have a very simple proof system where proofs may be easy to find, but they will be very long even in reasonable cases. Or you can have a very strong proof system that allows for many short proofs, but it will be much harder to find them. Sometimes it all comes down to adding or removing a single important rule, such as the cut rule in Gentzen’s sequent calculus:

Still, these results usually come in the form of counterexamples that one has to actively search for. There is no result that says that interesting mathematical theorems such as Fermat’s last theorem or the Riemann conjecture have to have astronomically long proofs, even in a simple proof system. And surely, even if the hardest riddles of mathematics do indeed turn out to be hard for a reason, there’s still a lot we can do about simpler problems, right? Math is large, it has a long frontier, and there should be plenty of opportunities to advance it.

As soon as computers allowed people to try, automated theorem provers did appear. In fact, in the early days of artificial intelligence logic was thought to be one of the key components. The famous 1943 paper by William McCulloch and Walter Pitts, which introduced the first mathematical model for a neuron and hence a neural network, was called “A logical calculus of the ideas immanent in nervous activity”, and the main results were purely logical in nature. McCulloch and Pitts compared several possible architectures of neural networks and established logical equivalences between them: if a function can be realized by one kind of network then it can also be realized by another. Just read the abstract if you don’t believe me:

Logic was a key idea in early AI: people thought that the difficult part of getting a machine to think would be to imbue it with logical reasoning, teaching it how to make inferences correctly. It soon became evident that reasoning in the everyday sense of the word is not a problem, and the real problem is converting murky everyday notions into statements you could reason with. Understanding notions such as “near” (as in “don’t go too near”) or “elevated” (as in “you have elevated blood sugar”) gave rise to fuzzy logic, converting a collection of pixels on a photo into a mathematical representation of a 3D object is the fundamental problem of computer vision, and so on.

Still, what about harder reasoning like proving new theorems? One of the first successful automated theorem provers was Logic Theorist, developed in 1956 by Allen Newell, Herbert Simon, and Cliff Shaw (see also Gugerty, 2006). It pioneered many techniques that are now standard. Formulas were represented as trees, and the search for a proof itself was a tree with the initial hypothesis as the root and deductions as branches. Since the search tree (unlike the final proof, which is just one of its paths) would definitely be exponential in practice, Newell, Simon, and Shaw developed heuristics for pruning branches unlikely to lead to a solution, a technique that would become standard throughout early AI. Finally, to implement Logic Theorist the authors developed a programming language called IPL (Information Processing Language) which was the direct predecessor of John McCarthy’s Lisp!

They tested Logic Theorist on Principia Mathematica, feeding it with 52 theorems from Chapter 2, in the same order. When Logic Theorist proved a theorem, it could add it to storage for use in later proofs. As a result, it proved 38 of the 52 theorems (73%!), and sometimes produced shorter proofs than the ones by Whitehead and Russell themselves!

In the 1950s, it was hard to expect this automated search to actually come up with new theorems: computers were slow and their memories were small. Still, these results were extremely promising. Logic Theorist is widely regarded as the first real life program from the field of AI, actually predating the famous Dartmouth workshop where the term was coined. In January 1956, Herbert Simon told his graduate class: “Over Christmas, Al Newell and I invented a thinking machine”, and he would later write that they “invented a computer program capable of thinking non-numerically, and thereby solved the venerable mind-body problem, explaining how a system composed of matter can have the properties of mind”.

The 1950s were indeed a very optimistic time. But where did this line of thinking lead? How did later attempts at theorem proving go?

Symbolic computation and formalized mathematics

In the 1960s and 1970s, the researchers’ attention turned to a large extent to symbolic math systems. One of the pioneers here was MACSYMA, which stands for “Project MAC’s SYmbolic MAnipulator” (Pavelle and Wang, 1985; Fateman, 1982). Project MAC (Machine-Aided Cognition or Multiple Access Computer) was an MIT lab that later grew into MIT CSAIL (Computer Science & Artificial Intelligence Laboratory), one of the leading academic AI labs today. MACSYMA was a software system, developed in a specially designed Lisp dialect, that could perform many symbolic mathematical operations including limits, derivatives, Taylor series, Laplace transformations, ODEs, and more. It was a direct precursor to such systems as Matlab and Maple, but it was mostly used as a computational tool for researchers in other fields of science.

Automated theorem proving, on the other hand, progressed much slower. One of the early landmarks here was the Automath formal language developed by Nicolaas de Bruijn in the late 1960s. Automath has been largely forgotten now, but it actually laid the foundations for typed lambda calculus, including the introduction of dependent types, and pioneered the use of the Curry–Howard correspondence, also known as the “proofs-as-programs” correspondence: a program of a certain type (in the sense of typed programming languages) can be seen as a proof of the proposition represented by this type. I won’t go into a detailed explanation here but do recommend the interested reader to work through at least the example given in Wikipedia.

One of the first popular proof assistants was Mizar, a system that first appeared in 1973 and is still in active use today. Then came Coq itself, which remains the popular proof assistant to this day. Another important proof assistant is HOL, which stands for “higher order logic”; indeed, HOL can handle higher-order logic proofs, and it is still a live project with new versions coming out. 

Today, there are plenty of tools that can verify formal proofs of mathematical theorems, and some of them can look for new proofs too. Naturally, there have been attempts to formalize at least the math that we already have… but without much of a success.

For example, there is a valiant effort in the form of the Formalized Mathematics journal established in the 1980s. It publishes formal, mechanically verified proofs of known mathematical results; naturally, nobody prohibits authors from using a computer to come up with the proofs either. Right now, some of the latest papers in Formalized Mathematics are solutions to problems from the book “250 Problems in Elementary Number Theory” by Wacław Sierpiński, published in the late 1960s. These are not open problems, they are just somewhat advanced problems for students that you might find in a textbook (here is a paper from Dec 31, 2023). 

I’m not saying this to kick Formalized Mathematics, I’m saying this to show that doing math in a formalized and automatically verifiable way is hard indeed, much harder than an outside view on math might suggest. The “QED Manifesto”, a similar initiative put forward in 1993, also quickly dissolved. In general, formalized mathematics still lags very far behind “real” mathematics done by people.

Automated theorem provers, i.e., programs that can try to find proofs all by themselves, do exist. For instance, there is a well-known family of first-order provers developed at the Argonne National Laboratory in Illinois, starting from Otter and continuing via EQP (Equational Prover) to Prover9. More modern examples include Lean, a general-purpose theorem prover and proof assistant.

And they are indeed used in mathematics (see, e.g., the list of papers using Lean), but full-fledged automated proofs are very rare and always constrained to cases where human mathematicians did see the path to a proof, but the path was too cumbersome to do by hand. One famous example here is the Robbins conjecture, proven in 1996 by the EQP prover. Again, I recommend the reader who is familiar with basic mathematical structures such as Boolean algebras to actually read through the problem setting by the link. The Robbins conjecture is about an alternative set of axioms for Boolean algebras, and the question is as close to axioms as possible: is the alternative set actually equivalent to the definition? In 1996, William McCune proved that it is indeed the case, using the EQP theorem prover that specializes on rewriting equations. You can find the whole proof in human-readable form in this paper by Allen Mann, although “human-readable” may be a slight overstatement in this case.

So this was a success for automated theorem proving. But this problem has the perfect combination of traits for the point I want to make:

• it is very close to the axioms (in fact, it’s a question about whether one set of axioms is equivalent to another);
• it is about a relatively simple object: there are few axioms, few connectives, and few derivation rules;
• but at the same time, the proof is quite long and hard to break down into meaningful lemmas, so for a human it is very hard to find by hand.

These traits are characteristic of most mathematical results where computers have been able to meaningfully assist humans. One of the first famous examples is the four color theorem, a conjecture from graph theory that you can paint the regions of any map in four colors so that no two regions painted in the same color share a nonzero border (arbitrarily many regions can come to a single point, of course, but that doesn’t count). As you can see, this is also a short and discrete kind of statement, but the proof (announced by Appel and Haken in 1976) was still done almost entirely by hand. The crucial point, however, required enumeration and analysis of about 1500 different cases, so this part was programmed and done on a computer. It’s not quite the automated proof search you would expect (although in 2005, the proof was actually formally verified in Coq, so the four color theorem is now part of formalized mathematics).

Other examples (see, e.g., this list on Wikipedia) are usually of the same nature: computers help with long case-by-case analysis or with mechanical rewriting of complicated equations, but the ideas remain human. In fact, many mathematicians are still wary of computer-assisted proofs because they are unverifiable by humans and therefore don’t fulfill the main function of a proof: they don’t convince people. In a paper on the Robbins problem, Louis Kauffman sums this conundrum up as follows: “Can a computer discover the proof of a theorem in mathematics?.. I say that a proof is not a proof until a person is convinced by it. In fact a mathematical proof is exactly an argument that is completely convincing to  a mathematician! In this sense, a computer does not, can not produce a proof… It does not know the proof. It only finds the steps. It is a human judgement that propels the result of the computer’s search into a statement that the computer has “found a proof”… If we judge that to be a proof, then it is a proof (for us)”.

But all that was in the 1980s and 1990s. Now we have powerful GPUs, deep neural networks that do wonders, exceeding the human level in many tasks that we considered purely human before. So they can help us with math as well… right?

Deep learning and mathematics

As we have already discussed, there are two main directions in how AI can help mathematics: either directly by finding proofs or indirectly (but usually more efficiently) by doing straightforward but cumbersome stuff like rewriting equations or doing case-by-case analysis.

Several breakthroughs have been made in following the latter strategy. Modern deep learning adds another important twist on this idea: instead of mathematicians writing code that enumerates possibilities, an AI model can try to write the best code for the problem as well. This is very similar to neural architecture search (NAS) that yielded some of the best neural architectures in computer vision, new activation functions, and more. Similar to how you can search for architectures, you can also search for programs, usually with some kind of genetic programming approach since computer programs are naturally represented by trees.

So you can take it one step further and tackle problems where the answer is an algorithm. In 2022, DeepMind’s AlphaTensor made the news doing exactly that: it discovered improvements in matrix multiplication algorithms, improving over Strassen’s algorithm for the first time in 50 years. In AlphaTensor, the tensor specifies which entries to read from the input matrices, and where to store the result; for example, in the three-dimensional tensor below, (a₁, b₁, c₁) and (a₂, b₃, c₁) entries are set to 1, and this means that c₁=a₁b₁+a₂b₃:

AlphaTensor optimized over such tensors with an MCTS-based algorithm very similar to AlphaZero that plays chess and Go but with some new advances related to the extra large width of the search tree in this case. As a result, it improved over the best known matrix multiplication algorithms for a number of different matrix sizes, starting from as low as 4×4 matrices; this is more than just a constant improvement since these algorithms can be applied recursively to handle block matrices of arbitrary size. This was a very important result, and it was obtained virtually independently of humans; but again, this falls more into the “searching through cumbersome cases” category, the AlphaZero-based search algorithm just helps scale it up to a previously unheard of number of cases.

Another important example in the same direction that made the news last year was AlphaDev, another work by DeepMind in a similar vein that managed to improve sorting algorithms, that is, the cornerstone of almost every data manipulation computer program in the world! In a Nature paper by Mankowitz et al. (2023), the researchers presented another AlphaZero-based modification of MCTS search designed to invent new sorting algorithms. The resulting algorithms have already been implemented in the std::sort C++ library, which means that they are already making millions of computer programs run faster.

As large language models became available, another direction appeared: you could ask LLMs to prove theorems directly! Naturally, it did not work all that well at first, and even today, if you just ask an LLM to prove a theorem, this strategy won’t get you published in Annals of Mathematics.

One way to improve here is to fine-tune LLMs on mathematical content. For example, Minerva (Lewkowycz et al., 2022) did just that, fine-tuning general purpose LLMs from the PaLM family on technical content. As a result, Minerva could successfully reason through some high school level mathematics, although it was still a far cry from proving new results. Here is a sample of what Minerva was capable of:

Another approach would be to use the already excellent coding capabilities of LLMs. As you know, modern LLMs can produce correct code snippets, so if your problem can be solved by some kind of enumeration you can ask the LLM to write this code for you. ToRA (tool-integrated reasoning agent) by Gou et al. (2023) closed the loop in this reasoning, using an LLM to write code, then going to an external tool to run it, and then fixing the code and interpreting the results with an LLM again. In the illustration below, the authors contrast ToRA with pure language-based and pure code-based approaches:

Finally, I want to highlight another work by DeepMind (looks like they are the main players here): “Advancing mathematics by guiding human intuition with AI” by Davies et al. This work pursues a very different approach to helping mathematicians: instead of trying to formally prove something, here the authors use machine learning to discover new possible relations between mathematical objects. Here is the general framework of how it works; note that there are both “computational steps” done by AI models and “mathematician steps” done by real people:

For example, the authors could discover and then actually prove a relationship between algebraic and geometric invariants in knot theory. The margins of this post are too narrow to explain what exactly this means, but in essence, a machine learning model detected that there might be a relationship between one way to describe knots in topology and another. This connection turned out to be real, and mathematicians were able to prove its existence and introduce new important objects that describe it. Naturally, they did it by hand, but their intuition in formulating this result was guided by ML-produced discoveries.

And with that, we have reached the latest news: FunSearch. It is yet another Nature paper by the DeepMind team, in this case adding some large language models into the mix. Let’s see how it works!

FunSearch: As fun as it sounds?

We now come to the actual result that motivated me to write this post. In December 2023, DeepMind researchers Romera-Paredes et al. published a paper called “Mathematical discoveries from program search with large language models”. They proposed a relatively simple way to use large language models to guide the search for new mathematical results, not in the form of actual results like most researchers have done before but in the form of programs that could generate these results. It goes like this: given a problem specification,

• first ask a pretrained LLM to generate some candidate programs that might solve the problem;
• add the resulting programs to the database of programs created, run them and score their results according to the desired objective function;
• then form a prompt that combines a few of the top scoring programs and asks the LLM to improve over them,
• and then feed this prompt to the LLM again, thus closing the loop.

Here is an illustration from the paper itself:

Specification includes an evaluation function that scores the solutions and a “solve” function that provides the barebone algorithm (say, a greedy search) and lets the LLM concentrate on the creative part (for greedy search it is the priority function that compares elements). Sounds pretty simple, and looks like it is: it is more of a prompt engineering result than a new machine learning approach.

So what could FunSearch do? One of the main results in this paper are new bounds for the cap set problem. Fields medalist Terence Tao, by many accounts the best mathematician alive, once called it “perhaps my favourite open question”, so let’s dive into the problem a little bit.

A cap set is a set of numbers in a finite field that does not contain nontrivial arithmetic progressions, i.e., where no three points form a line in the finite geometry of F₃ⁿ, where F₃ is the field of three elements… I started out on the wrong foot, didn’t I?

There is a much more accessible description of what’s going on in the cap set problem. You’ve probably heard of the card game “Set” where players need to shout out “Set!” when they see three cards such that for each of the four attributes—number, color, shape, and shading—the three cards are either all the same or all different. In the example below (taken from here, as well as the general idea of this connection), on the left you see two examples of sets, one where no attribute matches and another where almost all of them do, and on the right you see a sample Set board layout with one set highlighted (are there more? see for yourself):

In these terms, a cap set is a collection of cards that contain no sets, and the main question is this: how many cards can you lay down so that they contain no sets? For the original game of Set, the answer is known: back in 1971, Giuseppe Pellegrino proved that there exist collections of 20 cards without a set, but 21 cards always contain one (note that this result predates the invention of the game in 1974, so if there is any connection, the causality here goes in the opposite direction). But in mathematics, you always ask the more general question. Here, we generalize the number of attributes: how many cards with n different attributes (instead of 4 in Set) can you lay down without a set of three cards?

It is obvious that you can have 2ⁿ cards without a set: just pick two values for every attribute and use only cards with these attributes. It was proven in 1984 that the upper bound is asymptotically less than 3ⁿ, actually at most O(3ⁿ/n). For over 20 years, the gap between these two results remained a glaring hole in combinatorics; in fact, closing this gap was what Terence Tao called his “favourite open question” back in 2007.

Important progress was made in 2016 when Ellenberg and Gijswijt used the method developed by Croot, Lev, and Pach to reduce the upper bound to 2.756ⁿ; it is telling that both papers were published in Annals of Mathematics, the most prestigious venue for publication in pure math. Since then, there has been no improvement in the exponent for either lower or upper bound.

So what did DeepMind do with the problem? Fun search could provide a new upper bound on the cap set problem for n=8, i.e., it could produce a larger collection of Set cards with 8 different attributes and no sets on board than ever before.

Here is a general illustration where in the top middle we have an illustration for the cap set problem in terms of finite geometry (colors denote lines in F₃³), on the bottom we have the FunSearch results with a new record for dimension 8, and on the right you can see the program that generates this solution:

The program is virtually unreadable, and we will not analyze it here, of course, but it is still important that it’s a program, not just an answer in the form of a cap set. By analyzing this program, mathematicians can gain some insight into how this counterexample is structured; Romera-Paredes et al. did just that and could indeed understand the result better and relate it to other known examples in combinatorics.

Still, all this sounds a bit underwhelming: looks like FunSearch is still just searching for counterexamples, like countless helper programs for mathematicians before. It is still unclear when we are going to have a program that actually does new math in the form of proving theorems.

Conclusion

Today, we have discussed the main avenues for how AI can help mathematicians:

• direct automated theorem proving via first- and higher-order logic;
• helping with the cumbersome side of mathematics: enumerating special cases, doing automated case-by-case analysis, rewriting equations and so on;
• applying large language models to try and generate proofs and/or write code that will do the cumbersome parts instead of writing this code by hand;
• discovering new patterns in data, including data in the form of mathematical objects, that may inform the intuition of mathematicians and lead to new discoveries;
• using some combination of the above: for example, FunSearch uses an LLM to write key portions of programs that are then tested against the problem.

But if we put all this together, we basically get the full picture of making mathematics. Let us go back to the picture I started with, the general workflow of a professional mathematician, and put some of the papers and tools we have discussed in their proper places:

As you can see, AI is already helping mathematicians every step of the way, so maybe the “unreasonable ineffectiveness” I started with is not so ineffective after all. Still, it looks like doing math formally is hard, and so far the latest AI research can help somewhat, but only so much; there is no silver bullet that would just short-circuit the whole workflow and replace human mathematicians entirely. But we have also seen that doing formalized mathematics is hard for people too, even with the help of computers, so maybe there are deeper reasons here too.

On the other hand, AI progress is very fast right now. Two weeks after FunSearch, another DeepMind paper appeared in Nature: Trinh et al.’s “Solving olympiad geometry without human demonstrations”. They present a system able to successfully solve geometry problems from the International Mathematical Olympiad at nearly a gold medalist level; geometry problems virtually always require formal proofs, and IMO problems usually require quite ingenious ones. 

Note also that Nature has a very fast but nontrivial review cycle: the IMO geometry paper was submitted in April 2023, and the FunSearch paper was submitted in August 2023; this is more than half a year of progress already made since these results, and in 2023, half a year counted for a lot. So just like in most other fields, we probably won’t be expecting a really working theorem prover right until it appears.

And finally, I would like to take this opportunity to dedicate this post to my first research supervisor, Professor Nikolai Vavilov (not to be confused with his ancestor, the famous geneticist Nikolai Vavilov), who was a key figure in modern algebra, founded a thriving research school, wrote several very interesting textbooks, and lit up every conversation with his wit and erudition. I owe Nikolai Alexandrovich a lot in my mathematical upbringing. Tragically, Prof. Vavilov passed away last September.

Sergey Nikolenko
Head of AI, Synthesis AI

Here at Synthesis AI, we have decided to release the “Generative AI” series in an e-book form; expect a full-fledged pdf with all the images soon. But when I started collecting the posts into a single coherent whole, I couldn’t help but feel the huge, glaring omission of the most important topic in modern AI, the secret sauce that drives the entire field of ML nowadays: self-attention layers introduced in the original Transformer architecture. I haven’t planned to cover them before since there are plenty of other excellent sources, but in a larger format Transformers have become an inevitability. So today, I post the chapter on Transformers, which seems to be by far the longest post ever on this blog. We will discuss how the Transformer works, introduce the two main families of models based on self-attention, BERT and GPT, and discuss how Transformers can handle images as well.

The Transformer Architecture and Self-Attention

The Transformer was introduced in 2017, in a paper by Google Brain researchers Vaswani et al. with a catchy title “Attention is All You Need”. By now, it is one of the most important papers in the history of not only machine learning but all of science, amassing nearly 100000 citations (by Google Scholar‘s count) over a mere five years that have passed since its publication.

An aside: for some unknown reason, it is quite hard to Google the most cited papers of all time, and there is no obvious way to find them on Google Scholar. I have found an authoritative review of the top papers of all time in Nature, and it cites only three papers with over 100K citations in the entire history of science, but those are “proper” citations counted by the Web of Science database. Lowly arXiv preprints do not register at all, so their numbers are always far lower than on Google Scholar that counts everything. In any case, the Transformer paper is truly exceptional. 

There have been dozens of surveys already, so I will cite a few but it is far from an exhaustive list: (Zhou et al., 2023; Wolf et al., 2020; Lin et al., 2022; Tay et al., 2022; Xu et al., 2023; Wen et al., 2022; Selva et al., 2023). The Transformer was indeed a very special case, an architecture that, on one hand, uses ideas already well known in the machine learning community for many years, but on the other hand, combines them in a whole that has proven to be much, much larger than its parts. So what is the basic idea of a Transformer?

First, the original Transformer was an encoder-decoder architecture intended for sequence-to-sequence problems, specifically for machine translation. In essence, the original Transformer was designed to:

• first encode the input sequence (say, a sentence in French) into a latent representation, i.e., a dense vector of features in some highly semantic latent space;
• then decode the latent code into the new output sequence (say, a sentence in English).

This means that before starting to encode text, the Transformer needs to convert it into a sequence of tokens; we will talk about it more in the next section, and for the images here let us just assume that tokens are individual words. After that, the original Transformer had the following structure:

• an embedding layer that encodes input tokens into dense vectors;
• six encoder layers that produce semantically rich latent representations of input tokens;
• six decoder layers that produce the output in an autoregressive way, using the input tokens’ latent representations as conditions.

Here is this structure:

Each layer has a very simple internal structure:

• given some input vectors , an encoder layer first puts them through a self-attention layer followed by layer normalization, modifies the result with a feedforward layer, and outputs the resulting vectors  to the next encoder layer;
• after all encoder layers are done, we have the results in the form of all vectors output by the last encoder layer;
• item then each decoder layer puts its inputs  through a masked self-attention layer, then an encoder-decoder attention layer that actually looks at encoder outputs, and then a feedforward layer again;
• finally, when all decoder layers are done, the resulting vectors are fed through a very simple classification head—just one linear layer followed by a softmax—to produce the next token; it is then embedded into the next vector , and the decoding process can begin again, autoregressively.

Here is what the Transformer looks like with a single layer expanded in both encoder and decoder:

Layer normalization (Ba et al., 2016) is just a standard technique to stabilize training in deep neural networks; in the Transformer, it is also combined with a residual connection, so it is actually , where  is the matrix of original input vectors  and  is the matrix of the self-attention results . A feedforward layer is just a single layer of weights applied to the vectors .

The real magic happens in the self-attention layers, both in regular self-attention and encoder-decoder attention layers featured in the decoder. Let us look at them in more detail.

The intuition for self-attention layers comes from information retrieval, a field that we have already considered in detail in Part IV of this series. For the Transformer, we only need the very basic intuition of searching in the latent space, as illustrated below:

In this simple form, information retrieval works as follows:

• both queries and documents share the same latent space, although the ways of encoding them into this latent space may be different (after all, even if both queries and documents are texts they have very different properties);
• a search query (text queries shown on the top of the figure above) is put through a query encoder to get to the latent space;
• documents (represented by images in the figure) are also represented in the same latent space via a different encoder;
• to find the most relevant documents, we simply find the nearest neighbors for the query in the latent space among the documents; one often assumes that the latent space is linear and the distance metric there is just the scalar product of vectors,

     

In the self-attention layer, this intuition comes alive in a very abstract fashion. Let us follow through this process as it is illustrated below:

The self-attention layer receives as input a sequence of vectors , which we can think of as a matrix .

First, what are the queries, keys, and documents? All three of them come from the vectors  themselves! The figure above shows this idea with the example of what happens with :

• multiplying  by a weight matrix , we get the query vector ; note that the matrix  does not have to be square, and the dimension q of the query vectors, , may be different from (usually lower than) the input dimension , ;
• multiplying every by a second weight matrix , we get the key vectors for ; since we want queries and keys to inhabit the same latent space, we have the keys with the same dimension as queries, , so ;
• finally, the third weight matrix gets us the value vectors for; these are the documents that we will “retrieve” by their keys ; in this case we might have a different space for the documents, so formally we have a different dimension v for the values,  and ; in practice, however, one usually takes .

The matrices , , and  comprise the bulk of trainable weights in the self-attention mechanism. After applying them as above, we obtain three vectors from each input vector . Then we do the retrieval part, computing attention scores as scalar products between queries and documents. The figure above shows this process schematically with the example of  transforming into  for all different i. Then we need to rescale , dividing it by the square root of , and pass the scores through softmax to turn them into probabilities. The self-attention weights are thus

   

where are all the keys combined in a matrix, .

Then we use the result as coefficients for a convex combination of values . Thus, overall we have the following formula for what  turns into:

   

where  are all the values combined in a matrix, .

The normalizing factor comes from the fact that if you add q random numbers distributed around zero with variance 1, the result will have variance , and the standard deviation will be the square root of . So if you add 64 signed numbers that are around 1 in absolute value, the result will be around 8. It would be easy to saturate the softmax with this extra factor, so to get the numbers back to a reasonable range we divide back by the standard deviation.

We can combine the computation of each  shown above into a single formula in matrix form, which is how self-attention is usually defined:

   

But this is only one way to “look at” the input vectors! What we have defined now is not the full self-attention layer but only a single self-attention head. We want to parallelize these computations along different heads, using different weight matrices , , and to allow the Transformer layer to consider different combinations of the same input vectors at once.

This process, known as multi-head attention, is illustrated below:

Note that after H parallel heads, we get H output matrices , each of dimension . We need to compress them all into a single output matrix with the same dimension as the input matrix  so that we can stack such layers further. The Transformer does it in the most straightforward way possible, as shown in the figure: let us just concatenate them all into a single large matrix and then add another weight matrix  that will bring the result back to the necessary dimension:

   

With the output weight matrix , we allow the self-attention layer to mix up representations obtained from different attention heads; this is also an important way to add more flexibility and expressiveness to the architecture.

We are now entirely done with the self-attention layer but not quite done with the entire architecture. We have already discussed the rest of an encoder layer: after the multi-head attention, we use layer normalization with a residual connection and then add a feedforward layer that mixes features inside each of the token representations, with another residual connection around it leading to another LayerNorm, as shown inside the encoder layer in the general figure above.

This has been the most important part, but there are still quite a lot of bits and pieces of the Transformer architecture to pick up. In the next section, we will discuss how the decoder part works, how the input embeddings are constructed from text, and what the original Transformer architecture actually did.

Odds and Bits: Decoder, Tokenization, Positional Embeddings, and Discussion

We have discussed the main idea of self-attention and seen how it comes together in the encoder part of a Transformer. Let us now turn to the right part of the general figure shown above that has two more layer types that we do not know yet: masked self-attention and encoder-decoder attention. Fortunately, they are both now very easy to introduce.

Masked attention basically means that since the decoder works autoregressively, it should not peek at the tokens that it has not produced yet. This could be done by changing the input, but it’s easier and faster to just have the whole sequence and masking future positions inside self-attention layers themselves. Formally this means that in the self-attention formula, we set the softmax arguments to negative infinity for future tokens, which means that their attention weights will always be zero.

Encoder-decoder attention is a variation on the self-attention mechanism that takes into account the results of the encoder. These results are vectors with the same dimension as the output matrix  that we obtained in the formula above, that is, L vectors of length d, and the figure suggests that each layer in the decoder receives these vectors as a condition. 

It might seem to require a very different architecture to condition self-attention on this matrix… but in fact it’s an almost trivial modification. We have the exact same self-attention layer described above, with weight matrices that create queries, keys, and values for every attention head, but use different vectors as input:

• to create the queries, we use vectors from the previous layer, i.e., current representations of already generated output tokens;
• but for the “documents” in our “retrieval” task, i.e. for the key and value vectors, we use the vectors from the decoder.

Informally, this means that we are doing “retrieval” on the encoder’s output with queries made of already produced tokens. Formally, we simply use the same formula with queries, keys and values defined above, and all dimensions match nicely: there are L terms in the softmax argument for each vector, but the number of queries and hence number of outputs matches the number of inputs.

Note also that the decoder has an extra linear layer at the end followed by a softmax for next token classification; this is about the simplest classification head possible, obviously needed for the decoder.

But this is still not all. We need to discuss one more thing: how does the input text turn into a sequence of dense vectors that self-attention layers process so skillfully? There are two things to discuss here.

First, tokenization. I have mentioned above that tokens do not really correspond to words. In most Transformer-based models, tokenization is done with a process known as the byte-pair encoding, an interesting idea in its own right based on optimal coding theory such as, e.g., Huffman coding. To begin with, we consider all words present in the input text (the notion of a “word” should be understood liberally, but it is, more or less, a sequence of characters delimited by whitespace) and count the number of their occurrences, building a vocabulary. Let us consider a few words that share a lot of repeating character subsequences:

We first count the word frequencies, as shown above. Then we break down this vocabulary into individual symbols and count them; in practice there would be extra symbols for the beginning and/or end of a word and all sorts of extra stuff, but let’s keep it simple and stick to our “cat on a mat” example; this is the middle part of the figure above.

This is our original vocabulary of symbols, and now the encoding process can begin. We break down the symbols into pairs and count their occurrences:

{ ca: 10, at: 27, pe: 12, et: 12, ma: 5, ra: 8, ea: 4, ts: 4 }.

Then we choose the most frequent pair—in this case “at“—and re-encode it with a single new symbol that is added to the vocabulary; let’s call it Z. After that, we have a new set of words in the new encoding, and we can count the symbols and their pairs again:

{ cZ: 10, pet: 12, mZ: 5, rZ: 8, eZs: 4 },

{ c: 10, Z: 27, t: 12, p: 12, e: 16, m: 5, r: 8, s: 4 },

{ cZ: 10, pe: 12, et: 12, mZ: 5, rZ: 8, eZ: 4, Zs: 4 }.

At this point, we can choose the new most frequent pair—in this case “pe” or “et“—and replace it with another new symbol, say Y. Replacing “pe“, we get the following new vocabulary and statistics:

{ cZ: 10, Yt: 12, mZ: 5, rZ: 8, eZs: 4 },

{ c: 10, Z: 27, Y: 12, t: 12, e: 4, m: 5, r: 8, s: 4 },

{ cZ: 10, Yt: 12, mZ: 5, rZ: 8, eZ: 4, Zs: 4 }.

As we run the algorithm in a loop, new symbols may also become part of new pairs; in our example, the next most frequent pair is “Yt“, so after the next step we will have a whole separate token corresponding to “pet“. Note that we never remove symbols from the vocabulary even if they have zero occurrences after a merge: we may not have any t‘s left after the next merge, but new input text may contain new unknown words with t‘s that will need to be processed, so we need the vocabulary to stay universal.

The encoding process can be stopped at any time: on every step, we get a new extended set of tokens (vocabulary) that compresses the original text in a greedy way, and we can stop and use the current set of tokens. So in practice, we set a target vocabulary size and run the algorithm until the set of tokens reaches this size, usually getting excellent compression for the original text in terms of these new tokens. As a result, words may still be broken into parts, but the most frequent words will get their own tokens, and the parts themselves may have meaning; for example, in English it would be expected to have a token like “tion” appear quite early in the process, which is a frequent sequence of letters with a clear semantics.

That’s it for tokenization! At this point, the input is a sequence of fixed discrete objects (tokens) taken from a predefined vocabulary of size V. It remains to turn it into a sequence of dense vectors , which is usually done via an embedding layer that’s just basically a large matrix that consists of trainable weights. In earlier days of the deep learning revolution in natural language processing, word embeddings were a quite interesting field of study in and of themselves because they used to be trained separately and then just applied as a fixed “dense vocabulary” that neural models trained on top of. This field of study has given us word2vec (Mikolov et al., 2013a; 2013b; Le, Mikolov, 2014), GloVe (Pennington et al., 2014), and many more interesting ideas… but there is no point to discuss them here because now it’s just a trainable layer like any other, and the whole architecture is being trained at once, including the embedding layer.

Still, there is another point about the embeddings which is unique to Transformers. One of the main characteristic features of the Transformer architecture is that every input token can “look at” any other input token directly, with no regard for the distance between them in the input sequence. The self-attention layer has a separate attention weight for every pair of tokens, not just neighboring ones or something like that. This has a drawback too: the length of the input, which for language models is known as the context window, automatically becomes bounded. But this is a big advantage over, say, recurrent architectures where you need to go through every step of the sequence, “losing memory” along the way, before the influence of one word can reach another.

But there is another interesting consequence of this property: since the attention weights cover all tokens uniformly, we lose the sequence. That is, for a self-attention layer there is no sense of some tokens being “next to each other” or “closer in the input sequence”, it is all just a single matrix of weights. We need to give the Transformer an idea of the input sequence artificially; this is done via the so-called positional encodings.

Positional encodings are vectors added to the embedding that reflect where in the sequence the current token is; we will discuss them briefly but I also refer to a more detailed description of positional encodings by Kazemnejad (2019). How could we encode the position? Well, we could have a number that is increasing with the position but it is hard to get right:

• if we just used an increasing sequence like 1,2,3,…, it would not generalize to sequences longer than the usual length in the training set, and the network’s behaviour would be much less well defined for large values;
• if we used a given interval, say , and broke it down into the necessary number of pieces, then the positional encoding would have no idea how many words are actually there between two tokens: the distance from 0 to ½ could be one token or one hundred.

Therefore, the Transformer uses a very clever idea inspired by how we encode numbers in our regular positional notation. Consider a sequence of numbers, say written in binary, like on the left of the figure below:

As the numbers increase, the value of each digit forms a periodic function, with different periods for different digits in the number. We want to replicate something like that in the positional encodings, but since we have the full power of real numbers available now, we use continuous periodic functions, sine waves:

   

where pos is the token position in the sequence and d is the embedding dimension. This means that each cell in the has a sine wave with respect to the position (half of them shifted to a cosine wave), each with its own period that is increasing with i, that is, with the cell index. The result is shown in the figure above on the right, where the horizontal axis shows the cell indices i and the vertical axis shows token positions from top to bottom. Sine waves become more and more elongated (with increasing period) as we go from left to right, so for 20 tokens we are actually using only about 20-25 dimensions for the positional encoding, but this definition can support arbitrarily long input sequences, even longer than those present in the training set.

It was a little surprising to me that positional encodings are not concatenated with regular embeddings but rather added to them. It looks counterintuitive because positional information is different and should not be mixed with token semantics. But embeddings are learned rather than fixed, and as you can see in the figure, positional encodings take up a small portion of the overall vector, so they can probably coexist just fine. In any case, the input embedding is a sum of the trainable embedding for the current token and the vector PE(pos, i) defined above.

And with that we are completely done with the Transformer architecture, so let us briefly discuss its original results. As I have already mentioned, the original Transformer presented by Vaswani et al. (2017) was doing machine translation, and numerically speaking, results of the original Transformer architecture were not the most striking: the encoder-decoder architecture applied to machine translation scored roughly on par with the best existing models in English-French and English-Deutsch translations. But the Transformer had equally good BLEU scores in machine translation… while requiring 100x less compute for training! And when you have an architecture with 100x less compute, in practice it means that you can train a much larger model (maybe not exactly 100x larger, but still) with the same computational budget, and then you will hopefully scale to much better results.

Since 2017, Transformers have become one of the most popular architectures in machine learning. In the rest of this post, we will discuss some further extensions and modifications that the Transformer has undergone, although surprisingly few have been necessary to adapt the architecture even to entirely new data modalities.

Cutting the Transformer in Two: GPT and BERT

As we have discussed in the previous section, the basic Transformer is a full-scale encoder-decoder architecture, where the encoder produces semantically rich latent representations of text in the input language, and the decoder turns them into text in the target language by writing it autoregressively.

From there, it was only natural to cut the Transformer in two:

• we need semantically rich latent representations of high-dimensional input data for a lot of tasks, so we could use the Transformer encoder separately from the decoder to produce these representations;
• we need good language models that can produce text autoregressively, so we could use the Transformer decoder separately from the encoder to train a language model.

Let us begin with the latter, i.e., with the decoder, but first let us understand in slightly more detail what we are talking about.

A language model is a machine learning model that predicts the next token in a sequence of language tokens; it is easier to think of tokens as words, although in reality models usually break words down into smaller chunks. The machine learning problem here is basically classification: what is the next token going to be? A language model is just a classification model, and by continuously predicting the next token, a language model can write text. We have already discussed it in Part VII of the series:

The only thing a language model can do: predict the next token, over and over. Note that this also means that there are very few problems with data collection or labeling for general-purpose language models: any human-written text becomes a set of labeled examples for supervised learning because the language model just predicts the next word, which is already there in the text. Therefore, you can just collect a lot of text off the Web and train on it! There are several standard datasets that are used to train large language models (LLMs) nowadays:

• the Common Crawl corpus is a free and open repository of data crawled off the Internet, with over 250 billion Web pages downloaded over more than 15 years; it is a huge and varied corpus that has been used for over 10000 research papers, including modern large language models such as GPT-3, LLaMA, or T5 (Raffel et al., 2020);
• since the Common Crawl is so huge and diverse, there have been many attempts to refine it, choosing subsets suitable for different tasks; in particular, the C4 dataset (which stands for “Colossal Clean Crawled Corpus”), with about 380GB of text (360 billion tokens) in the cleaned up version and 2.3TB unprocessed, was prepared in 2019 for training the T5 model and remains a very popular dataset derived from Common Crawl;
• the Pile (Gao et al., 2020) is a freely available corpus with 825 GiB of English text, with an emphasis on diversity: in addition to a specially filtered subset of Common Crawl (Pile-CC), it combines several academic sources such as arXiv and PubMed, source code crawled from GitHub, available datasets of full-scale books, programming-related discussions from StackExchange, and many smaller data sources;
• finally, although these datasets actually aim to be all-encompassing downloads of the entire Web (perhaps cleaned up and filtered in different ways), work on creating new datasets is still far from over; for example, the RefinedWeb dataset (Penedo et al., 2023) has been released very recently (June 2023) and claims that with some additional preprocessing and filtering, the resulting dataset extracted from Common Crawl (the authors claim about 5 trillion tokens in the full version and release publicly a subset of 600 billion tokens) can result in even higher-performing LLMs.

And now that we have these huge datasets, the language modeling part appears to be trivial: let us just use the Transformer decoder to autoregressively predict the next token! This exact idea was implemented in a series of models called Generative Pre-Trained Transformers — yes, that’s the famous GPT family.

In particular:

• the original GPT (Radford et al., 2018) had 12 layers in the Transformer decoder part, with 12 masked self-attention heads each and 64-dimensional states; it was pretrained on the BookCorpus dataset (Zhu et al., 2015) with over 7000 books (a tiny dataset by modern standards!) and then fine-tuned for specific tasks with labeled data; the authors reported that BookCorpus was chosen so that the model would learn to handle long-range dependencies better;
• GPT-2 (Radford et al., 2019), released in February 2019, was more or less a direct scale-up of GPT, pretrained on the same BookCorpus dataset and a newly collected WebText dataset with 8 million web pages vetted by humans: they scraped outbound links from Reddit that obtained at least 3 karma (40GB of text in total); the largest version of GPT-2 had 48 layers and dimension 1600, for a total of about 1.5 billion parameters, 10x of the original GPT;
• GPT-3 (Brown et al., 2020), released in June 2020, scaled things up by two more orders of magnitude; its largest version, known as the davinci family, had an unprecedented size of 175 billion parameters; GPT-3 became the basis for further models such as ChatGPT that we have already discussed in Part VII.

As the GPT family scaled up, it also obtained more impressive generalization abilities with regard to problems you might want to solve with it. Suppose, for example, that you wanted to recognize entailment relations, that is, find out whether a hypothesis sentence follows from a premise sentence. Data for this problem, e.g., the popular MultiNLI (Multi-Genre Natural Language Inference) corpus (Williams et al., 2018) looks like pairs of sentences labeled with three kinds of results:

In the example above, for a premise “Two dogs are running through a field” (I took this example from Gugurangan et al., 2018),

• the hypothesis “There are animals outdoors” gets the label “Entailment“, i.e., it follows from the premise,
• the hypothesis “Puppies are running to catch a stick” is labeled “Neutral” since while there is no direct contradiction, the dogs might or might not be puppies, and the stick is not necessarily there as well,
• and the hypothesis “The pets are sitting on a couch” is a clear “Contradiction“, i.e., the premise rules it out.

Different versions of GPT and BERT would handle the entailment problem differently. To adapt the original GPT (Radford et al., 2018) or BERT (Devlin et al., 2018) to a specific task, you had to fine-tune it, i.e., modify its weights by performing additional training on the downstream task; you had to fine-tune the GPT model with a separate entailment dataset by encoding the dataset into a special form and training new weights for a separator embedding and a new linear layer on top. The figure below shows how this would work for the original GPT and details what new weights have to be learned. This is the way such problems had been processed in deep learning before, e.g., with large-scale recurrent architectures (Rocktäschel et al., 2015).

Starting from GPT-2, and definitely in GPT-3, developers of Transformer-based architectures moved to a different approach, where no new weights need to be trained at all. Similar to multitask learning and following an earlier attempt by the MQAN (Multitask Question Answering Network) model (McCann et al., 2018), they noted that a variety of different tasks could be encoded into text. Actually, one could argue that the Turing test is so good exactly because you can sneak in a lot of different questions into text-only conversations, including questions about the surroundings, the world in general, and so on. So to make use of a language model’s “understanding” (in this post, I’m putting “understanding” in quotes, but have you seen Part VIII?) of the world, you could give it a few examples of what you need and frame the problem as continuing the text in the prompt. The following figure compares the two approaches (GPT on the left, GPT-2 and 3 on the right) and shows a sample prompt for the logical entailment problem on the right; you would probably obtain better results if you put more examples in the omitted part of the prompt:

Note that in this approach, all that the language model is doing is still predicting the next token in the text, nothing more! Moreover, it is not even trained to do new problems such as entailment or question answering, it already “understands” what’s needed from its vast training set, and a short prompt with a couple of examples is enough to summon this “understanding” and let the model solve complex semantic problems.

A different way to cut up the original Transformer was introduced in the BERT model developed by Google researchers Devlin et al. (2018) . BERT stands for Bidirectional Encoder Representations from Transformers. As the name suggests, the main emphasis here is on learning semantically rich representations for tokens that could be further used in subsequent models, somewhat like word embeddings such as word2vec and GloVe had been used before but better and with full context available to the model producing representations.

To do that, BERT leaves only the encoder part of the Transformer, the part that produces a semantically rich representation for each of the input tokens. But how do we train it if not with the language modeling objective that GPT uses? It turns out that we still can do approximately the same thing: instead of predicting the next token, we can mask out some of the tokens in the input (in the same way as we mask future tokens in the decoder) and predict them based on the full context from both left and right. This is known as masked language modeling, and it is the main pretraining objective for BERT.

Here is a comparison of the BERT (left) and GPT (right) pretraining objectives:

Just like language modeling itself, masked language modeling has a long history; it was originally known as the cloze procedure, introduced in 1953 as a readability test for texts in a natural language (Taylor, 1953). The word “cloze” is not a last name, it was derived from “closure”, as in gestalt psychology: humans tend to fill in missing pieces. So if you want to compare how “readable” two texts are, you delete some pieces from them at random and ask people to fill in the blanks: the most readable passage will be the one where the most humans get the most missing pieces right.

The original BERT combines two variations of this idea:

• masked language modeling itself, where tokens to be predicted are chosen at random, and 
• predicting an entire next sentence of tokens, which helps the model make its representations more semantically rich and more oriented towards the global context.

In later research, more models have been developed based on the Transformer encoder that can provide different flavors of embeddings with somewhat different properties. We will not do a proper survey here, referring to, e.g., (Zhou et al., 2023; Wolf et al., 2020; Lin et al., 2022), but let us mention a few of the most important BERT variations that have been important for natural language processing applications:

• RoBERTa (Robustly optimized BERT pretraining approach; Liu et al., 2019) is one of the most widely used modifications; they found that the original BERT was under-trained and fixed it, switched to the byte-level BPE tokenizer that we discussed above, and made a few more tricks to improve pretraining while keeping the architecture itself intact; when people need good pretrained token embeddings to plug into a neural model, they usually take RoBERTa embeddings; there are several different model sizes to choose from;
• BART (Bidirectional and Autoregressive Transformers; Lewis et al., 2020) turns the Transformer into a denoising autoencoder: it pretrains by corrupting the text and reconstructing the original through the Transformer decoder; although it is a full-scale encoder-decoder architecture I put it here because BART is used in practice very similarly to BERT: you use the semantically rich intermediate representations and discard the denoising decoder because in real life you seldom need to actually denoise corrupted sentences;
• ALBERT (A Lite BERT; Lan et al., 2019) applied several techniques to reduce the number of parameters in a Transformer and make training faster while trying to preserve the expressiveness as much as possible; you can probably train ALBERT yourself on a desktop and harness the power of BERT for your own private dataset;
• DistilBERT (Sanh et al., 2019) moved in the same direction with model distillation techniques, again targeting a model that you can fine-tune with customer-grade hardware;
• and so on, and so forth, with dozens of derivative models proposed in literature (Ganesh et al., 2021; Kalyan et al., 2022; Patel et al., 2023; Rogers et al., 2020; Xu, McAuley, 2023) and available, e.g., in the HuggingFace transformers library.

BERT and its derivative models such as RoBERTa have proven to be a very valuable tool for natural language processing (Patwardhan et al., 2023). The usual way to apply BERT has been to take the vectors it produces (BERT embeddings, or RoBERTa embeddings, or ALBERT, or any other) and plug them into standard neural models for various natural language processing tasks. This has usually improved things across the board, in problems such as:

• text classification where one usually takes either the embedding of the special symbol at the beginning or end of the text or all BERT embeddings and applies a simple classification head on top of it (Khadhraoui et al., 2022);
• the same applies to other tasks that reduce to text classification such as sentiment analysis, irony detection, and others (Barbieri et al., 2020);
• for sequence labeling tasks such as named entity recognition, you also use Transformer-produced embeddings and an entity classification model on top, but this time the entity classification model may be more complex since we want to predict contiguous multi-word entities (Gu et al., 2021; Ji et al., 2020; Li et al., 2021);
• as for question answering and similar tasks that require writing free text, this is usually best served by the GPT family; in Part VII, we have discussed the capabilities of ChatGPT and GPT-4 that make a lot of tricks from prior research unnecessary; this is another example of the “bitter lesson” (Sutton, 2019), and you can decide for yourself whether this is a good thing or a bad thing.

Finally, another line of models that has been instrumental in modern NLP is XLM (cross-lingual language model; Conneau, Lample, 2019), a series of models based on BERT and GPT that trains on several languages at once. To do that, they apply byte-pair encoding to all language at the same time, getting a shared multilingual vocabulary, and use the same kind of LM and masked LM objectives to train in multiple languages at once. XLM and its successor models such as XLM-RoBERTa (Conneau et al., 2019) defined state of the art in many cross-lingual tasks such as the ones from XNLI, a cross-lingual benchmark for natural language inference (Conneau et al., 2018).

This has already turned into a high-level survey, so I think it is time to cut the survey short and just say that Transformers permeate absolutely all subfields and tasks of natural language processing, defining state of the art in all of them. But, as we will see in the next section, it’s not just natural language processing…

Vision Transformers

The Transformer immediately proved itself to be an excellent model for processing sequences of tokens. We will not speak of it in detail but sequences of other nature have also yielded to the magic of Transformers; for example, HuBERT soon became a standard model for speech processing (Hsu et al., 2021).

But images seem to be a different beast, right? An image has a natural two-dimensional structure, and deep learning has long had just the recipe for images: convolutional neural networks process every small window in the same way, sharing the weights in a form of ultimate structural regularization. Neural networks have been instrumental in the deep learning revolution, starting from AlexNet that made CNNs great again in 2011-2012 (Krizhevsky et al., 2012) and all the way to the automatically optimized architectures of the EfficientNet family (Tan, Le, 2019).

Well, it turns out that Transformers can help with images too! To do that, you need to convert an image into a sequence, and usually it is done in a very straightforward way. One of the first models that attempted it was Visual BERT (Li et al., 2019; Li et al., 2020), a model initially designed and pretrained for image captioning:

Since captions deal with objects that appear on an image, Visual BERT preprocessed the image with a fixed pretrained object detection system such as Faster R-CNN (Ren et al., 2015). Then the objects are cut out of the image, embedded into vectors via convolutional networks and special positional embeddings that indicate where the object was in the image, and just fed into a single Transformer:

The figure above also shows sample attention heads and how words from the caption actually do attend to the objects that they describe or are closely related to.

The pretraining process closely follows how the original BERT is trained. Visual BERT has two pretraining objectives: masked language modeling where the task is to fill in the blanks in the caption and sentence-image prediction where the model needs to distinguish whether a given caption matches the image or not.

Similar ideas have been developed in many different BERT-based variations. Let me just note one of them: VideoBERT (Sun et al., 2019) that applied similar ideas to video captioning and processing, including text-to-video generation and forecasting future frames in a video:

The figure above shows these problems: VideoBERT is able to predict the features of video frames corresponding to a given text (in this case a recipe), although it is, of course, better in the video-to-text direction, exceeding contemporary state of the art in video captioning. 

VideoBERT is again pretrained with masked language modeling on a sequence of both text captions and video tokens:

In this case, video tokens are obtained by sampling frames from the video, extracting features with a pretrained CNN, and tokenizing the features with simple k-means clustering. Both Visual BERT and VideoBERT were validated by experimental studies where they exceeded state of the art in visual question answering, image and video captioning, and other similar tasks.

But the most successful Transformer-based architecture for images has proved to be the Vision Transformer (ViT) developed in 2020 by Google researchers Dosovitsky et al. and introduced in a paper with a pithy title “An Image is Worth 16×16 Words“. Its original illustration from the paper is shown below:

ViT is again basically a very straighforward modification of BERT. The difference is that now the model does not use text at its input at all, restricting itself to image-based tokens. 

The input image into small patches: an image with channels becomes a sequence of patches , where is the number of patches that fit into the original image (see the illustration above). The patches are turned into embeddings via a simple linear projection, and then the resulting sequence is fed into a Transformer encoder just like BERT. For pretraining, ViT uses masked patch modeling just like BERT does, replacing half of the input embeddings with the same learnable [mask] embedding and aiming to reconstruct the mean colors of the original patches.

Similar to the original Transformer, ViT uses positional encodings to add information about the sequence. What is even more striking, it is the same positional encoding as in the regular Transformer even though the geometry is now two-dimensional. Dosovitsky et al. report their experiments with positional encodings that would reflect the two-dimensional structure, but, surprisingly, this did not make any significant difference: one-dimensional positional encodings that we discussed above worked just as well.

Since 2020, ViT has been used for numerous different applications (we refer to the surveys by Guo et al, 2021 and Khan et al., 2022) and has had several important extensions that we will not discuss in detail but have to mention:

• the Swin Transformer (Liu et al., 2021), where Swin stands for shifted windows, uses an idea similar to ViT but in a hierarchical fashion: it processes image patches on several scales, computing self-attention across patches in a convolutional-like architecture; as a result, it can scale up to larger input resolutions and can be adapted for dense recognition tasks such as image segmentation while the default ViT has to work with relatively large patches and cannot go down to the level of individual pixels needed for segmentation;
• a later iteration, Swin Transformer v2 (Liu et al., 2022), scaled the Swin Transformer up to 3 billion parameters and allowed for training with images up to pixels, further improving state of the art in image processing problems across the board.

Finally, another important architecture that has added important new ideas to the Transformer is DeepMind‘s Perceiver (Jaegle et al., 2021a). It is a general-purpose architecture that can process numerous different modalities: images, point clouds, audio, and video, basically of any input dimension. The problem that the Perceiver has to solve is the quadratic bottleneck of Transformer’s self-attention: the formulas we showed above for the original Transformer have quadratic complexity in the input size. Importantly, it’s quadratic in a very specific part of the input size: you can project the queries, keys, and values into smaller dimensions but there is no escape from having quadratic complexity in the number of queries, i.e., the context window size. 

The Perceiver avoids this bottleneck by using lower-dimensional latent units: it’s quadratic in the number of queries, so we use a small vector of latents for queries and can use large byte arrays as inputs for K and V, projecting them down to a lower-dimensional representation in cross-attention layers, as shown in the original illustration from Jaegle et al., (2021a):

The cross-attention layer is the same as in the Transformer decoder (see above).

The next version of Perceiver, called Perceiver IO (Jaegle et al., 2021b), extended this idea to outputs as well as inputs. While the original Perceiver could only solve problems with low output dimensions, such as classification, Perceiver IO can also handle large output arrays such as high-definition images. It is done with a trick reminiscent of how NeRFs represent high-dimensional outputs with implicit functions (Mildenhall et al., 2020; Tancik et al., 2023): Perceiver IO uses a smaller output query array to process with cross-attention and then constructs the actual output queries for the large-scale final output in an automated way, by combining a set of vectors that describe properties of the current output such as position coordinates. The general structure looks like this:

We will not go into more detail on this idea, but as a result Perceiver IO can handle high-dimensional outputs such as images or audio, which means it can scale to problems such as image segmentation, optical flow estimation, audio-video compression by autoencoding and so on.

In this series, we have used Vision Transformers in Part IV, where they served as the basic image encoders for the CLIP and BLIP models that will provide us with high-quality multimodal latent spaces for both multimodal retrieval and text-to-image conditional generation.

Conclusion

The idea of a self-attention layer, originally appearing in the Transformer encoder-decoder architecture in 2017, can be easily called the single most important idea in the last ten years of machine learning. Transformers have, pardon the obvious pun, transformed machine learning, getting state of the art results for all types of unstructured input data, including those that do not have an obvious sequential structure, like images that we have considered above.

Moreover, as we have seen in Part VII of this series, Transformers are becoming instrumental not only for the academic discipline of machine learning but also for the world economy. Transformative AI (TAI) that we have mentioned in Part VIII is named after an economic transformation similar to the Industrial Revolution, but it might prove to be yet another pun on the world’s most popular architecture.

Over the course of this “Generative AI” series, we have already taken Transformers and applied them in many different ways: generated discrete latent codes for VQ-VAE-based image generation models in Part III, mapped images and text into a common latent space in Part IV, encoded text to use it to condition diffusion-based models in Part VI, and upscaled straightforward language models from the GPT family into universal tools that find uses across many different industries in Part VII. Who knows, maybe Transformers will get us all the way to AGI, as we have discussed in Part VIII. In any case, it is hard to imagine modern machine learning without Transformers.

Sergey Nikolenko
Head of AI, Synthesis AI

This is the last post in the “Generative AI” series. Today, we look into the future and discuss where the current trends take us, what dangers might artificial general intelligence (AGI) hold for us, and whether we are ready for these dangers (spoiler: not at all). I will present the case for AGI doomers and discuss the main arguments, but please keep in mind that in this post, everything is mostly speculation (although there actually are attempts to put this speculation on firm mathematical ground).

AGI-related risks: a rough classification

We ended the last post on the differences between slow and fast takeoff speeds in AI development. But regardless of whether superhuman AGI comes overnight or several years after reaching approximately human level, it still may come pretty quickly even with respect to human timescales. We better be ready to face AGI in our lifetimes. Are we?

The previous post read as a glowing review of the latest developments, and that was intentional. In this post, let me posit right off the bat that the rise of large language models is worrying as much as it is exhilarating. Here is our plan for today, with a rough classification of different levels of potential risks related to human-level and ultimately superhuman intelligence:

We will begin with what AI researchers usually call “mundane problems”. These are the problems you already hear about on the news sometimes: modern large language models can be jailbroken and then start giving away dangerous information or insult users, modern image generation models can be used to create convincing deepfakes, AI models have biases that come either from the training data or the model architecture itself, and so on. These problems are not entirely new, but I’m positive we can either resolve them or at least become accustomed to them.

As AI becomes a larger part of the economy (which it almost certainly will), the risks grow as well. Even without reaching superhuman levels, AI is already a transformative technology, leading to a kind of new industrial revolution where many previous jobs may become obsolete. So far, transformations like this have been tumultuous but always ultimately positive: they have always created more and better jobs than they destroyed. Will this be the case for AI as well?

Finally, even the economy takes a back seat compared to existential risks. We humans are quite new to the idea: true, we have had nuclear weapons able to eliminate humanity (although not really), and the climate change may at some point approach an existential risk, but AI-related risks may prove to be very different, and we will discuss why.

We will end this last post with a brief overview of what people are currently doing about these risks through the emerging field of AI alignment research. In brief, we hope this research will arrive on time to save us all, but we are still far from a solution.

The “mundane problems”

The “mundane problems” are those you hear about when GPT-4 makes the news: AI posing as a human, deepfakes fooling real people with images or voice, and so on. We will see that AI-related dangers are far from limited to the mundane, but let us first consider those.

First, jailbreaking: the art of making a large language model disobey its explicit instructions (that have been fine-tuned into the model by its developers, probably by RLHF or similar techniques that we discussed the previous post) and exhibit some kind of antisocial behavior. All large language models that we discussed have been jailbroken in some way. You cannot rely on RLHF or other fine-tuning approaches if you are dealing with a determined adversary, so anything a LLM had been trained on can make it to its generated text. Microsoft’s Sydney was shut down after it started implicitly (and sometimes explicitly) threatening users:

Sydney was kind of a special case: its “niceness-inducing” RLHF was clearly done very sloppily, if at all. This kind of outburst may be harder to get in other models—but far from impossible. Here are, for instance, some jailbreaks for GPT-4. It is hard to say which actually work because they are constantly getting patched, but in essence many of them are variations on the DAN jailbreak (“Do Anything Now”) that was invented for ChatGPT. At some point you could (doesn’t work out of the box now) just paste this prompt and have ChatGPT get you “forbidden” answers while staying in character for DAN:

Deepfakes are still with us too. In the last post, we discussed how on May 22, a fake Twitter account posing as Bloomberg posted a fake photo of an explosion in the Pentagon complex in Washington DC, leading to an immediate $500B market cap swing. We are sure to expect more fake images, and more AIs posing as people. After all, the very paper introducing GPT-4 shows an example of the model passing a CAPTCHA test with human help:

These kinds of antics usually make the news because they are both easy to understand and easy to mentally extrapolate: what if everything you see on the Web is more likely to be a deepfake or AI-generated unverified text than not? I do not, however, want to spend too much time on the mundane problems because there’s nothing radically new in them: they are just scaling up already known human behaviors, and it seems that many of these problems already have solutions. For instance, to avoid deepfakes you might want to have trusted sources signing their images with some kind of cryptographic protocol, which would be just a small nuisance for the end user, and current crypto is probably secure enough even for a (somewhat) superintelligent hacker.

So while it is already taking a lot of effort to fine-tune language models out of this kind of behavior, in my opinion it’s not the crux of the problem. Let us move on to more interesting stuff.

Economic transformation: the AI industrial revolution

We move on from mundane problems that look like natural problems for any new and potentially somewhat dangerous technology to something more serious: the economic transformation that AI and AI-related solutions can bring. Mostly everybody agrees that AI, and especially AGI, has the potential to become at least as transformative as the Industrial Revolution.

This is not just a metaphor but a comparison that can be made numerical. In the report on “Forecasting transformative AI with biological anchors“, Ajeya Cotra operationalizes this analogy as follows: “Roughly speaking, over the course of the Industrial Revolution, the rate of growth in gross world product (GWP) went from about ~0.1% per year before 1700 to ~1% per year after 1850, a tenfold acceleration. By analogy, I think of “transformative AI” as software which causes a tenfold acceleration in the rate of growth of the world economy (assuming that it is used everywhere that it would be economically profitable to use it).”

Tenfold acceleration in the rate of growth would mean that the world GDP grows by 20-30% per year, that is, doubles approximately every four years. Cotra admits that “this is a very extreme standard”, but for the purposes of our discussion it still falls short of a full-scale technological singularity.

So far, this sounds great. What are the downsides? How about the jobs lost to AI?

Whole industries are being transformed by recent AI advancements, and it will definitely take some time for regulation or private contracts to catch up. As a characteristic example, let us consider the Hollywood actors’ and writers’ strike. The Screen Actors Guild – American Federation of Television and Radio Artists (SAG-AFTRA) noticed that actor contracts, especially for relatively unknown actors and extras, started to include clauses that allow the employers to “use an individual’s likeness for any purpose forever without their consent”.

These clauses had not been controversial when all they meant was that the movie company can include CGI in the scene and apply a filter to the photo. But soon they may mean that when you sign up as an extra, the movie company makes a scan of your face and body, pays you for this day of work, and then proceeds to include your digital avatar into all subsequent pictures with no additional payment to you. Naturally, the whole point of the strike is to amend these contracts, but still: how many actors do you really need if you can copy them from movie to movie?

The writers are in an even more precarious situation: large language models are already able to write scripts. So far their attempts have not been entirely successful but they are improving, and it’s very possible that soon a human writer will only have to pitch script ideas that get fleshed out by LLMs. See this paper by DeepMind for a detailed explanation of the state of the art in this regard (although this paper is from April 2023, so I’d imagine it’s already behind). 

Copywriting on the Web, where standards are lower and the vast majority of texts are rehashings, listicles, or short news items, is almost certain to be largely replaced by AI-generated text soon. This very blog would probably read better if I used GPT-4 to write the post from a detailed outline—but I’m old-fashioned, and have soldiered on by myself so far.

One could ask why this sounds like a problem at all. Humanity has dealt with new technologies before, and while it had sometimes been a bumpy ride it had always resolved itself for the better: more new jobs were created than lost, and the new jobs were less physical, less repetitive, and generally more “human”. As a result, new tech led to higher standards of living for the vast majority of people within a generation or two. The Luddite textile workers would sometimes indeed lose their jobs but on average the Industrial Revolution was a tide that raised all ships.

AGI, however, might be very different. At some point, especially if robotics improves further (right now it looks like a possible bottleneck), AI might be able to do everything that an average human could. Or, perhaps, everything that a human with an IQ under 100 was able to meaningfully contribute to society—that’s still half of us, by definition. Economies of scale will kick in: you can make AIs and robots cheaper but the cost of human labor will always have a lower bound because people need something to eat and to wear. When using AI becomes cheaper than this lower bound, it won’t be a matter of training for a new job or moving to a new place: for huge numbers of people there will be simply no way to constructively participate in the economy.

Still, the perspectives of job loss and a possible next societal transformation on the scale of the industrial revolution are not what I am afraid of. After all, making some (or most) humans obsolete comes with some pretty large benefits: working for humans, such powerful AIs will most probably solve many if not all of our health issues, create an economy of abundance, and make work unnecessary for most if not all people. But there is also another option for AGI to be far scarier than just another technological milestone; let’s discuss why.

The X-Risk

I’m not worried about the jobs. Or the deepfakes. Or foul language that a machine learning model might use online. What I’m worried about is that humanity is on the verge of creating an entity smarter than ourselves. Last time it happened with the apes and early hominids, and it did not go too well for them.

The standard argument, presented by Nick Bostrom in his 2003 book “Superintelligence”, involves a thought experiment about a “paperclip maximizer”, a superhuman AGI that is trying to improve the production of paperclips. It probably starts by improving some production processes at the paperclip factory, fully succeeds, and makes the factory into a marvel of optimization. The AGI creators are very happy at that point.

But then the AGI notices that there are other ways to increase the number of paperclips in the Universe—this is its only objective in the thought experiment. To further increase the number of paperclips, it would be useful to accumulate resources and make itself more powerful in the world. This is the effect known as instrumental convergence: basically whatever goal you set, you benefit your chances of achieving that goal by gathering power and resources.

Since the AGI is smarter than humans, it begins to accumulate resources in ways that are not obvious for us. A few iterations later the AGI notices that many more paperclips can be done if it takes the planet’s resources under full control. Humans are sure to get in the way so it deals with the humans first. Soon, the Earth is covered with two types of factories: paperclip factories and space docks that build spaceships to start producing paperclips elsewhere. And it all started with a performance optimizing AI:

Paperclips are just an example, of course. But still, at first glance this sounds dumb: why would the AGI do something stupid like that? Why would we program such a dumb objective function? There are several reasons:

• first, we don’t know how to specify an objective function that’s aligned with our values; the values are just too complex, and anything we can formalize is much simpler; we mathematicians know that functions are often optimized at extreme values of their arguments;
• second, instrumental convergence: whatever the final goal (even paperclips), it always helps to get power, get resources, protect yourself, and probably improve yourself, in particular make yourself smarter;
• third, the orthogonality thesis: the objective function and intelligence used to achieve it are orthogonal; that is, intelligent agents can pursue arbitrary (computable) goals, such as paperclip maximization or getting all humans to smile and say happy things; I’ll leave it to you to imagine how the latter can go horribly wrong.

Taken together, these reasons do not imply any specific scenario of our doom, and it would be pointless to go into specific scenarios. For instance, paperclip maximization does sound pretty far-fetched by itself.

But these three reasons do suggest that AGI, if and when it happens, will soon take over the world. Eliezer Yudkowski, whose voice of warning is now increasingly being heard (see the conclusion for a list of references), compares this reasoning to predicting how a chess game goes. If you or I sit down to play against a modern chess engine, nobody can predict how the game will go, which opening we play, and so on and so forth—there are astronomically many ways a chess game can go. What we can predict, quite certainly, is that the chess engine is going to win:

Similarly, you and I can think of millions of different scenarios of how events may unfold in case we develop a superintelligent AI. Each of these scenarios will be unlikely, but the endpoint appears to be that the AI wins, simply by virtue of being smarter and pursuing the goal of amassing power, which is an instrumental goal for everything else.

This may sound unreasonable at first glance: why wouldn’t the humans notice that the AI is going rogue and shut it down? Well, to continue the analogy, think about a chimp watching over a human who is making, say, a bow out of string and wood. Would the chimp realize what is going on before it’s too late? Why would we realize anything about an AGI that is actually smarter than us?

If that still does not look convincing, let us go through some standard counterarguments.

First, maybe the AI becomes humanlike, even superhuman, but so what? Albert Einstein was super smart, worked on nuclear physics, and he did not destroy the world. Unfortunately, there is no law of physics or biology saying that the human intellect is anything like the limit on cognitive abilities. Our brain sizes are limited by energy consumption and difficulties with childbirth. In examples of cognitive problems where learning is not limited to imitating humans, AI usually has no problem overcoming the human mastery level: think AlphaZero for chess and Go.

Second, sure, the AI may be smart and even secretly malevolent, but it’s sitting inside a computer, right? What if we just don’t let it out? Unfortunately, we are already letting AIs “out of the box”: people have been happy to provide AutoGPT with access to their personal email, the Internet, personal computers etc. An AI with access to the Web can ask people to do seemingly innocuous tasks, order material things to be 3D-printed, bacteria to be synthesized in labs from a DNA string… possibilities are endless even at the current level of technology.

Third, this all sounds like a challenge, and maybe you and I cannot solve these problems, but humans are a smart bunch. We have already invented many dangerous technologies but it all has worked out in the end, right? Including the A-bomb and the H-bomb? Well, yes, humans are good in science but making new stuff safe seldom works right at the first try. Henri Becquerel and Marie Curie died from handling radioactive materials, Chernobyl and Fukushima happened despite our best efforts to make nuclear energy safe, Challenger and Columbia disintegrated in flight… With AGI, there may not be a second chance, and we may not be able to contain the damage.

Finally, if we don’t know how to align AGI, why don’t we just stop short of building it? Nobody is arguing that GPT-4 is going to destroy humanity, and it already has many transformative uses, with new ones being invented every day; why don’t we stop at GPT-4 or maybe GPT-5? Sure, that would be a great solution, but how do we enforce it? It is unclear how long Moore’s law can continue but so far, customer-facing gaming GPUs of today are nearly equivalent to industrial-scale clusters of a few years ago. Nobody can prevent AGI from appearing if all it takes is a few GPUs thrown together in a garage. Containing the development of new hardware might be possible, but it is a coordination problem that requires joint effort from all countries, with no defectors trying to get ahead in any economic or military race by developing new AI techniques… you can see how this is rapidly becoming more far-fetched than a paperclip maximizer. In all probability, humanity will happily march on and create more and more powerful AIs right until the end.

That was bleak, right? Are there any answers?

What Can We Do? What Are We Doing?

There are several approaches that the AI community is currently exploring:

• interpretability studies, where we are trying to understand what’s going on inside large AI models with the hope that understanding will lead to control;
• AI safety, which is a term usually applied to fine-tuning LLMs or other AI models with techniques such as RLHF (reinforcement learning with human feedback);
• AI alignment, understood as aligning the values between AI and humans, that is, making the AI “understand” and “care about” human values rather than blindly optimizing paperclips.

Having interpretable AI models would help, but this field is also very difficult, and interpretability results are so far quite underwhelming. Modern large language models are black boxes for us, in about the same way that a human brain is a black box: we know how a single neuron works pretty well, and we know which part of the brain is responsible for speech recognition and which is the motor cortex, but that’s a very far cry from actually reading minds.

AI safety via RLHF and similar techniques may seem more successful; for instance, discovered jailbreaks usually do get patched. However, what we are actually doing to align current LLMs looks like just superficially “teaching them to behave” without any understanding of or control over the underlying processes. This is usually illustrated by the following meme image, where researchers are putting smiley faces on the Shoggoth (a Lovecraftian horror figure also featured in the title images for this section):

What we really want is AI alignment: making the potential AGI care about us and our values. This problem is usually broken down into two parts:

• outer alignment asks how to capture our values in a way understandable for AI models; if we design an objective function, are we going to be happy when it is actually optimized? and how do we design it at all? the paperclip example is one of the problems here;
• inner alignment is the problem of making the model actually optimize the objective function we design for it; this may sound tautological but isn’t: it is very possible, for instance, that the goals emerging during model training align with the objective on the training set but will diverge catastrophically when applied out of distribution.

Unfortunately, at present we have no idea how to solve these problems. In particular, there already exist many examples of outer alignment failures in the form of specifications gaming, that is, situations where the model is trying to optimize the objective function as stated but coming up with ingenious and undesirable solutions. Here is a list of them compiled by Viktoria Krakovna et al., including such examples as fooling a human evaluator by placing the robotic arm between the object (target for grasping) and the camera or power-seeking behavior found in existing large language models.

As for inner alignment, an interesting concept here is the Waluigi effect, named after the evil counterpart of Luigi in Nintendo’s Mario franchise. Suppose that we want to train a large language model (or another AI model) to exhibit some desirable behavior, for instance be nice to humans. It can achieve this goal in two different ways:

• either be genuinely nice to humans (Luigi)
• or behave nice to humans while secretly being anti-human (Waluigi).

The interesting observation here is that the latter option looks much more probable! The outward behavior is exactly the same: being nice to humans, so as long as the model is nice it may be in kind of a “superposition” between the two, not necessarily “choosing sides” yet. But “Luigi” is an unstable equilibrium: as soon as the model shows any undesirable behavior, it becomes more likely to be a “Waluigi” (double agent), and there is no way to get back since all “good” behavior is perfectly consistent with the Waluigi! 

Moreover, once you have a Luigi, all it takes to become a Waluigi is flipping one bit; I was speaking figuratively, of course, but it’s clear that it’s much easier (say, in terms of Kolmogorov complexity) to define something when you have already defined its exact opposite.

These are just two examples of the arguments that make AI alignment look extremely hard. For a far more exhaustive list, see “AGI Ruin: A List of Lethalities” by Eliezer Yudkowsky, the main spokesperson for the “AI apocalypse” scenario. He makes a convincing argument.

So what can we do now? Most researchers agree that we will have to solve the hard problem of AI alignment sooner or later, and the best we can do—apart from actually working on the problem—is to somehow contain and possibly even stall AI development until we make real progress. This reasoning, coupled with the staggering rate of developments in the AI spring of 2023, has already led to serious talks about government regulations about AI capabilities development. Here is how it happened (all the quotes are accurate):

AGI X-risk entered the public consciousness this spring. There have been meetings at the White House and hearings in the US Congress with key players from industry, including OpenAI CEO Sam Altman, Microsoft CEO Satya Nadella, and Google and Alphabet CEO Sundar Pichai. The industry leaders confirmed that they take AGI-related risks very seriously and commit to caution in advancing AI capabilities.

At the end of May, an open letter warning about AGI-related risks appeared, signed by thousands of researchers and other notable figures in the field of AI. The letter was quite brief:

I’m sure it was hard to find even a single sentence that everybody could agree on. Still, this sentence definitely captures the current mood of most people involved. There hasn’t been any actual legal action taken yet, but I guess that we can expect more regulation and, most importantly and most hopefully, a more careful approach to developing AI capabilities. Alas, we cannot know if it will help.

Conclusion

I hope the last part has not been too encouraging. AI alignment is a field still in its infancy, and it needs all hands on deck, now. So as a conclusion for this post, I wanted to list the key people working on AI alignment and related topics now and key resources that are available if you want to learn more about it:

• the main forum for all things related to AGI dangers and AI alignment is LessWrong, a rationality-focused portal where all of the people listed below publish regularly;
• Eliezer Yudkowsky is a key figure here; he has been warning us of superintelligent AI dangers for over a decade now, and I can’t recommend enough his magnum opus, the “Sequences” (not entirely about AI but excellent throughout), the above-mentioned “AGI Ruin: A List of Lethalities”, “AI Alignment: Why It Is Hard and Where to Start”, his recent post “Death with Dignity Strategy” (please take with a grain of salt), and of course, the wonderful “Harry Potter and the Methods of Rationality”;
• Luke Muehlhauser is a researcher working on AI alignment, in particular on AI-related policy matters at Open Philantropy; to get started I recommend his “Intelligence Explosion FAQ” and “Intelligence Explosion: Evidence and Import”;
• Paul Christiano is an AI alignment researcher who split from OpenAI to start his own non-profit Alignment Research Center; as a good intro to the field take a look at his “Current Work in AI Alignment” talk;
• Scott Alexander is not a computer scientist at all but his “Superintelligence FAQ” is an excellent introduction to the AI alignment problem and a great example of why his blog Astralcodexten (previously known as Slatestarcodex) is one of my all-time favorites;
• if you prefer listening, Eliezer Yudkowsky has been appearing on a number of podcasts recently where he has stated his position in detail; I recommend a 4-hour long interview with Dwarkesh Patel (time flies!), “EconTalk” with Russ Roberts, and a “Bankless” episode with David Hoffman and Ryan Sean Adams; the latter is especially interesting because the hosts clearly wanted to talk about crypto and maybe economic effects of AI but had to face the existential risk and respond to it in real time (in my opinion, they did a great job taking it seriously);
• finally, I have been following this AI spring mostly through the eyes of Zvi Mowshowitz, who has been publishing weekly newsletters on his blog; there have been over 30 of them already, and I also recommend his other work on the blog and at LessWrong.

And with this lengthy but hopefully illuminating post I conclude the whole generative AI series! It has been great to be able to talk through the most interesting developments in image generation over the past few years. Til next time!

Sergey Nikolenko
Head of AI, Synthesis AI