Our sixth installment of the NeuroNuggets series is slightly different from previous ones. Today we touch upon an essential and, at the same time, rapidly developing area — deep learning frameworks, software libraries that modern AI researchers and practitioners use to train all these models that we have been discussing in our first five installments. In today’s post, we will discuss what a deep learning framework should be able to do and see the most important algorithm that all of them must implement.

We have quite a few very talented junior researchers in our team. Presenting this post on neural networks’ master algorithm is Oktai Tatanov, our junior researcher in St. Petersburg:

What a Deep Learning Framework Must Do

A good AI model begins with an objective function. We also begin this essay with explaining the main purpose of deep learning frameworks. What does it mean to define a model (say, a large-scale convolutional network like the ones we discussed earlier), and what should a software library actually do to convert this definition into code that trains and/or applies the model?

Actually, every modern deep learning framework should be able to do the following checklist:

• build and operate with large computational graphs;
• perform inference (forward propagation) and automatic differentiation (backpropagation) on computational graphs;
• be able to place the computational graph and perform the above operations on a GPU;
• provide a suite of standard neural network layers and other widely used primitives that the computational graph might consist of.

As you can see, every point is somehow about computational graphs… but what are those? How does it relate to neural networks? Let us explain.

Computational Graphs: What

Artificial neural networks are called neural networks for a reason: they model, in a very abstract and imprecise way, processes that happen in our brains. In particular, neural networks consist of a lot of artificial neurons (perceptrons, units); outputs of some of the neurons serve as inputs for others, and outputs of the last neurons are the outputs of the network as a whole. Mathematically speaking, a neural network is a very large and complicated composition of very simple functions.

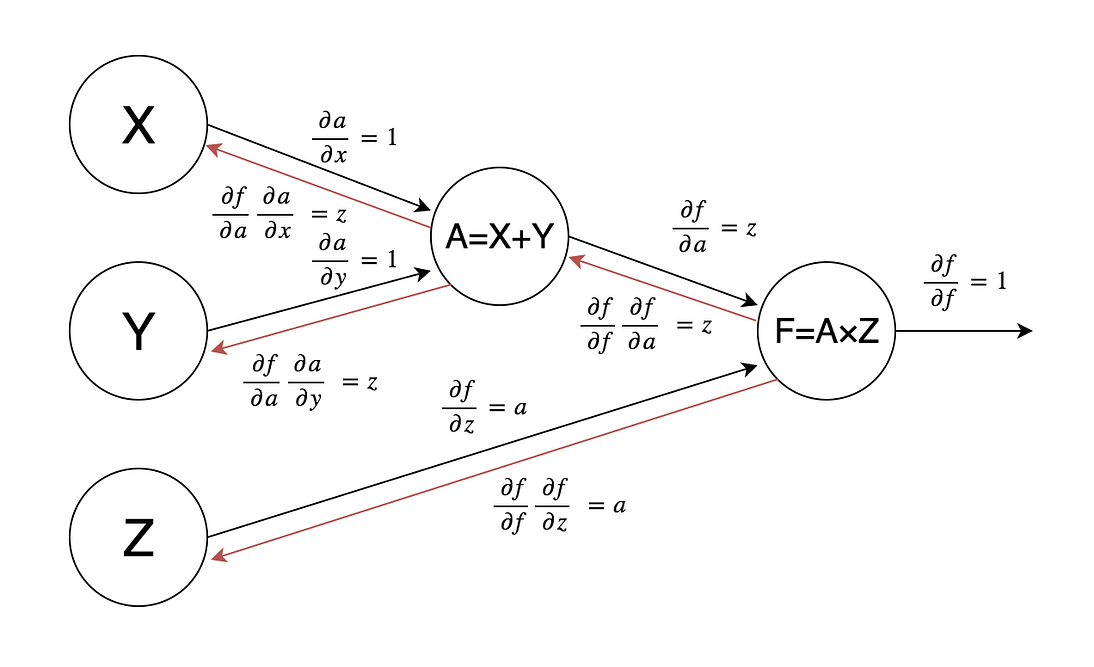
Computational graphs reflect the structure of this composition. A computational graph is a directed graph where every node represents a mathematical operation or a variable, and edges connect these operations with their inputs. As usual with graphs, a picture is worth a thousand words — here is a computational graph for the function :

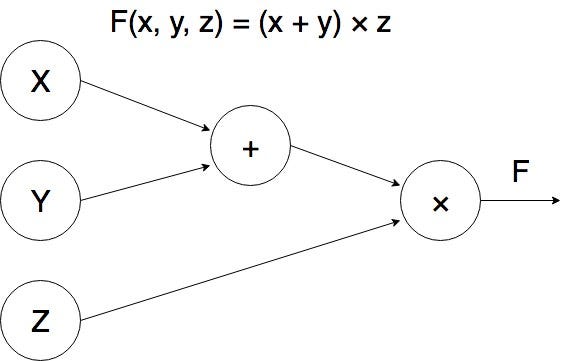
The whole idea of neural networks is based on connectionism: huge compositions of very simple functions can give rise to very complicated behaviour. This has been proven mathematically many times, and modern deep learning techniques show how to actually implement these ideas in practice.

But why are the graphs themselves useful? What problem are we trying to solve with them, and what exactly are deep learning frameworks supposed to do?

Computational Graphs: Why

The main goal of deep learning is to train a neural network in such a way that it best describes the data we have. Most often, this problem is reduced to the problem of minimizing some kind of loss function or maximizing the likelihood or posterior distribution of a model, i.e., we either want to minimize how much our model gets wrong or want to maximize how much it gets right. The frameworks are supposed to help with these optimization problems.

Modern neural networks are very complicated and non-convex, so basically the only optimization method we have for large neural networks is the simplest and most universal optimization approach: gradient descent. In gradient descent, we basically compute the derivatives of the objective function (the gradient is the vector consisting of all partial derivatives) and then go into the direction where the objective function increases or decreases, as needed. Like this:

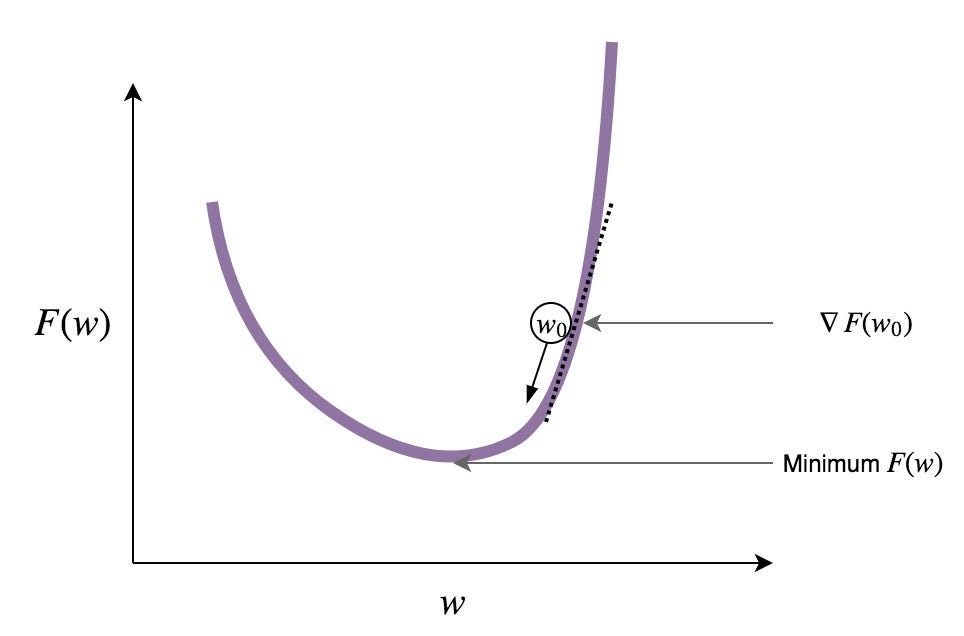
There are, of course, many interesting improvements and modifications to this simple idea: Nesterov’s momentum, adaptive gradient descent algorithms that change the learning rate separately for every weight… Perhaps one day we will return to this discussion in NeuroNuggets. But how do we compute the gradient if we have the neural network as model? That’s where computational graphs help…

Computational Graphs: How

To compute the gradient, deep learning frameworks use an algorithm called backpropagation (bprop); it basically amounts to using the chain rule sequentially across the computational graph. Let us walk through an application of backpropagation to our previous example. We begin by computing partial derivatives of every node of the graph with respect to each of its inputs; we assume that it is easy to do, and neural networks do indeed consist of simple units for which it is easy. Like in our example:

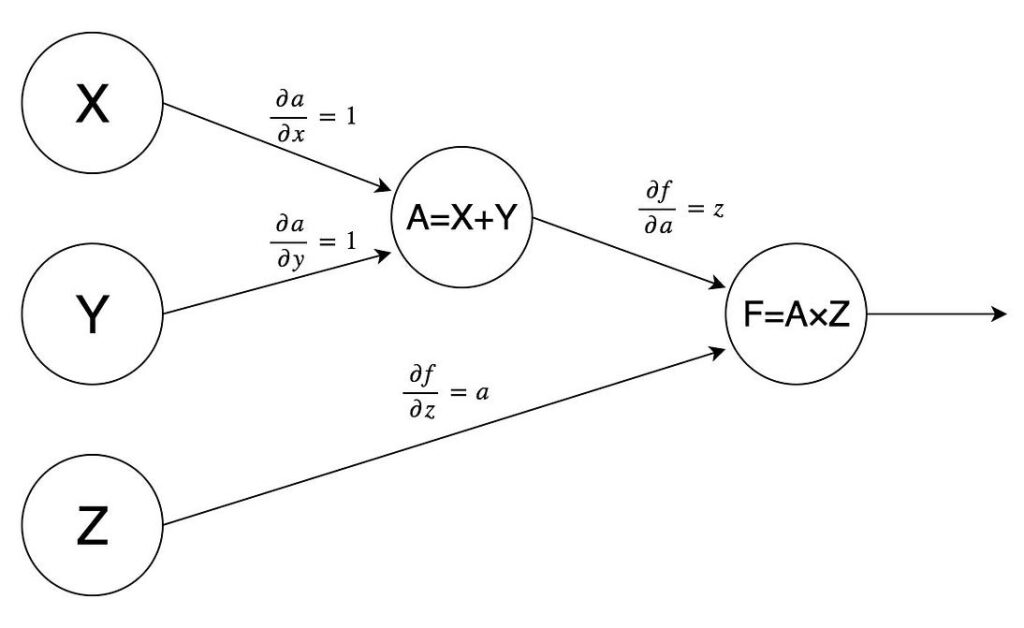
Now we need to combine these derivatives with the chain rule. In backpropagation, we do it sequentially from the graph’s output, where the objective function is computed. There we always have

   

Next, for example, we can get

   

since we already know both factors in this formula. Backpropagation means that we go through the graph from right to left, computing partial derivatives of f with respect to every node, including the weights that we are interested in. Here is the final result for our example:

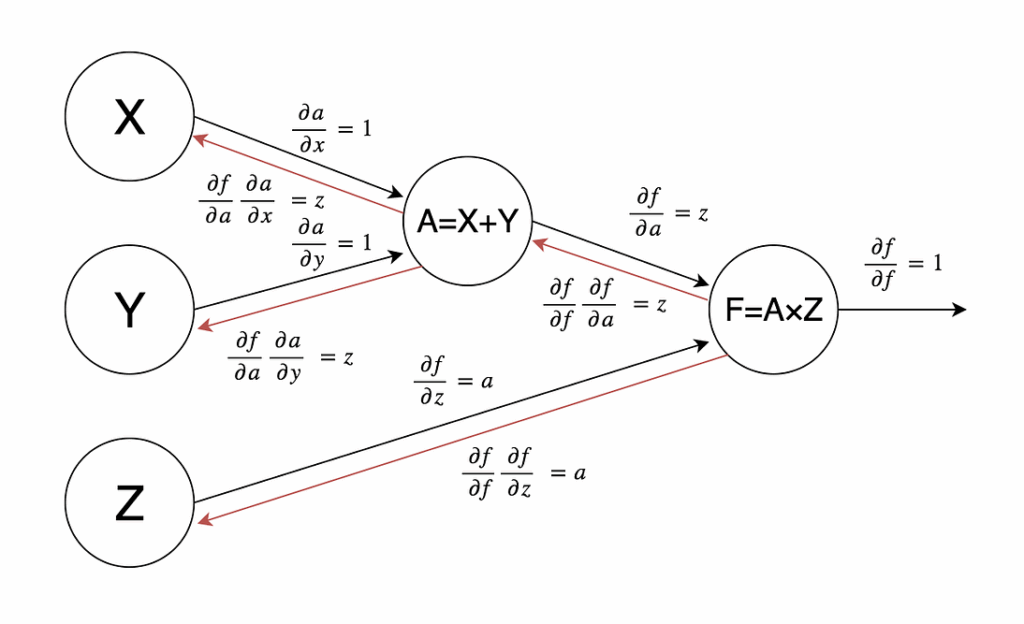
This very simple algorithm allows us to set up algorithms to train any deep neural network. This is exactly what any deep learning framework is supposed to do; they are in reality automatic differentiation libraries more than anything else. The main function of any framework is to compute and take derivatives of huge compositions of functions. Note, by the way, that to compute the function you also need to traverse the computational graph, but this time from left to right, from variables to the outputs; this process is called forward propagation (fprop).

Parallelizing the Computations

Once you have the basic functionality of fprop and bprop in your library, you want to make it as efficient as possible. Efficiency gains mostly come from parallelization: note that operations in one part of the graph are completely independent from what happens in other parts. This means, for instance, that if you have a layer in your neural network, i.e., a set of nodes that do not feed into each other but all receive inputs from previous layers, you can compute them all in parallel during both forward propagation and backpropagation.

This is exactly the insight that to a large extent fueled the deep learning revolution: this kind of parallelization can be done across hundreds or even thousands of computational cores. What kind of hardware has thousands of cores? Why, the GPUs, of course! In 2009–2010, it turned out that regular off-the-shelf GPUs designed for gamers can provide a 10x-50x speedup in training neural networks. This was the final push for many deep learning models and applications into the territory of what is actually computationally feasible. We will stop here for the moment but hopefully will discuss parallelization in deep learning in much greater detail at some future post.

There is one more interesting complication. Deep learning frameworks come with two different forms of computational graphs, static and dynamic. Let us find out what this means.

Static and Dynamic Computational Graphs

The main idea of a static computational graph is to separate the process of building the graph and executing backpropagation and forward propagation (i.e., computing the function). Your graph is immutable, i.e., you can’t add or remove nodes at runtime.

In a dynamic graph, though, you can change the structure of the graph at runtime: you can add or remove nodes, dynamically changing its structure.

Both approaches have their advantages and disadvantages. For static graphs:

• you can build a graph once and reuse it again and again;
• the framework can optimize the graph before it is executed;
• once a computational graph is built, it can be serialized and executed without the code that built the graph.

For dynamic graphs:

• each forward pass basically defines a new graph;
• debugging is easier;
• constructing conditionals and loops is easy, which makes building recurrent neural networks much easier than with static graphs.

We will see live examples of code that makes use of dynamic computational graphs in the next installment, where we will consider several deep learning frameworks in detail. And now let us finish with an overview.

Deep Learning Frameworks: An Overview

On March 10, Andrej Karpathy (Director of AI at Tesla) published a tweet with very interesting statistics about machine learning trends. Here is the graph of unique mentions of deep learning frameworks over the last four years:

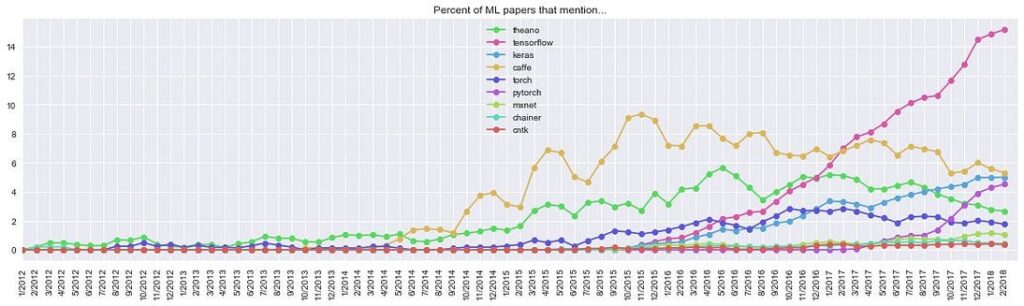
Unique mentions of deep learning frameworks in arXiv papers (full text) over time, based on 43K ML papers over last 6 years. Source: https://twitter.com/karpathy/status/972295865187512320

The graph shows that the top 4 general-purpose deep learning frameworks right now are TensorFlow, Caffe, Keras, and PyTorch, while, for example, historically the first widely used framework theano has basically lost traction.

The frameworks have interesting relations between them, and it is worthwhile to consider them all, get a feeling of what the code looks like for each, and discuss their pros and cons. This post, however, is already growing long; we will come back to this discussion in the second part.

Oktai Tatanov
Junior Researcher, Neuromation

Sergey Nikolenko
Chief Research Officer, Neuromation